Exploring Hyperbolic Functions

Mathematical Software. Mathematical Research. Mathematical Education. Tvalx Products.

Hyperbolic function are less known as trigonometric function. But at some level, in Complex Analysis, for example, they become necessary. Let's explore them with help of Math Center Level 2 . The notation for hyperbolic functions resembles notation for trigonometric functions: sinh, cosh, tanh, ctgh, sech, csch. Where h stands for hyperbolic.

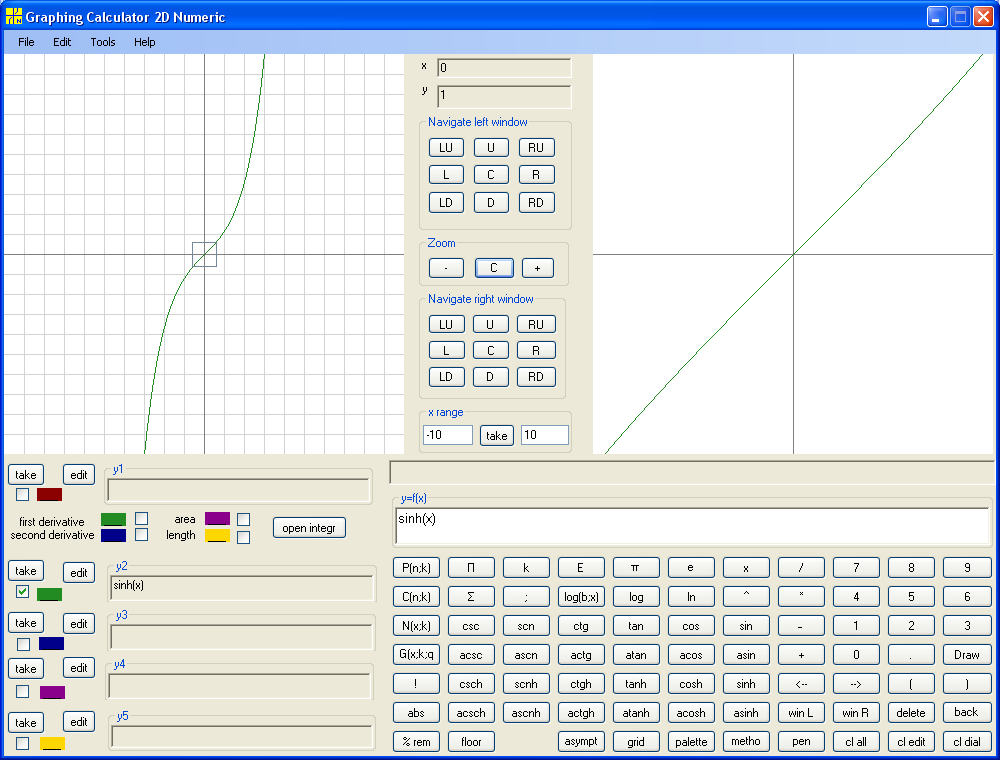
Consider y = sinh(x):

Visually sinh(x) reassembles sin(x) only at the origin.

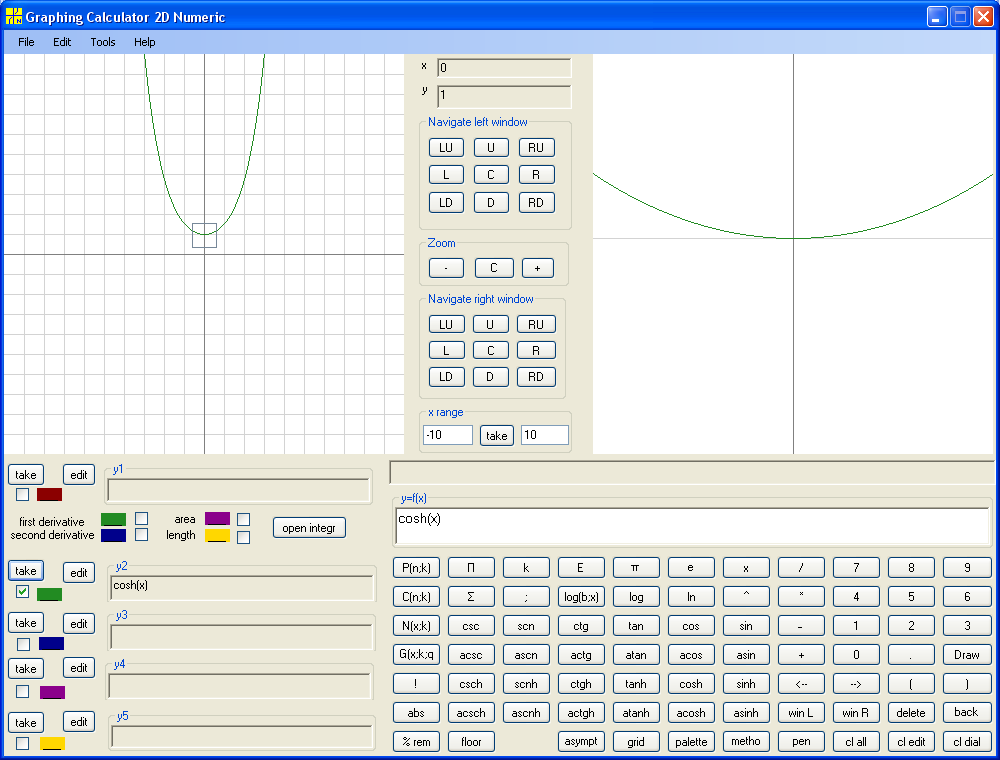
Consider y = cosh(x) :

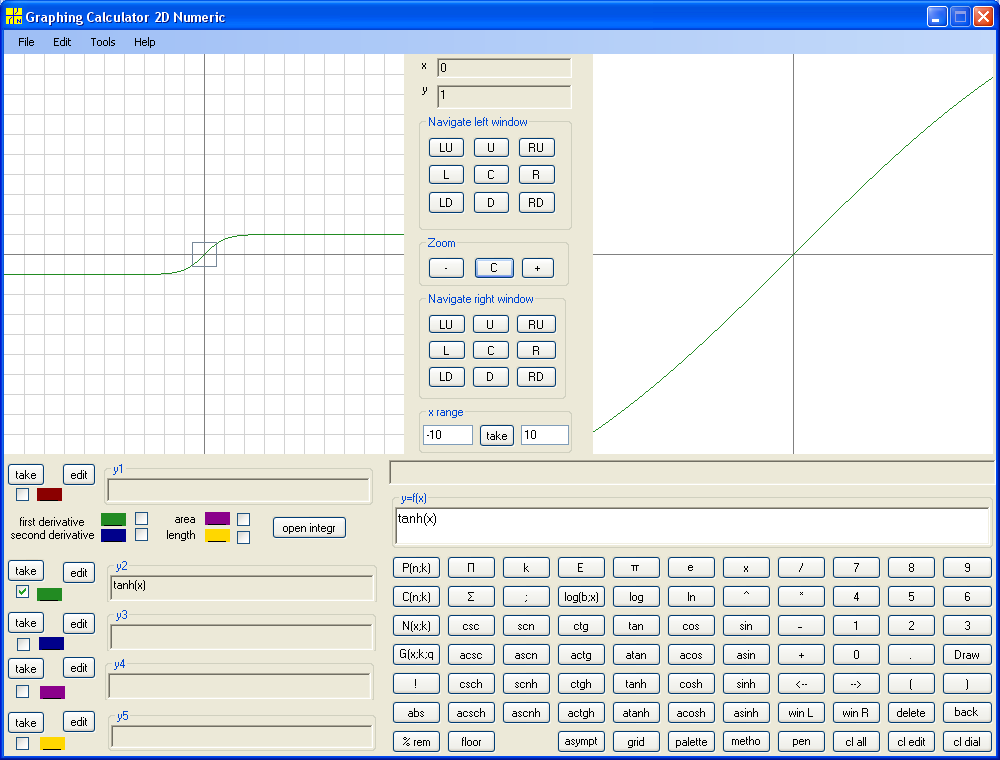
Consider y = tanh(x) :

Consider y = ctgh(x) :

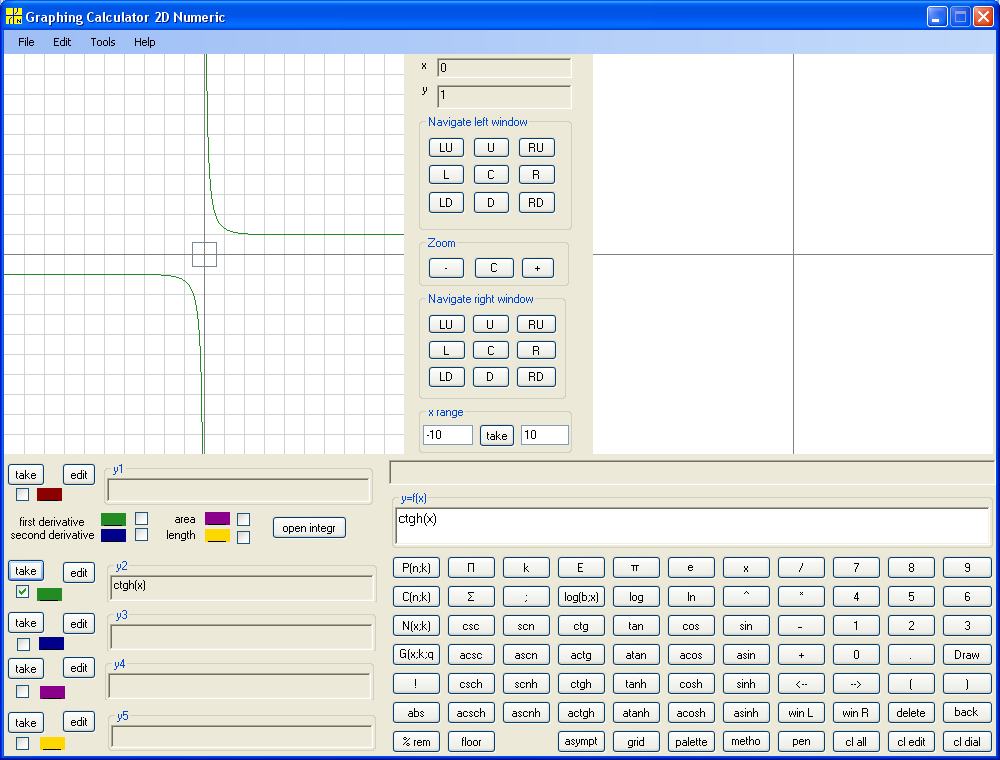
We see that hyperbolic functions are not periodic and their graph are not very similar to corresponding trigonometric functions. Let's explore numeric derivatives of hyperbolic functions.

y = sinh(x):

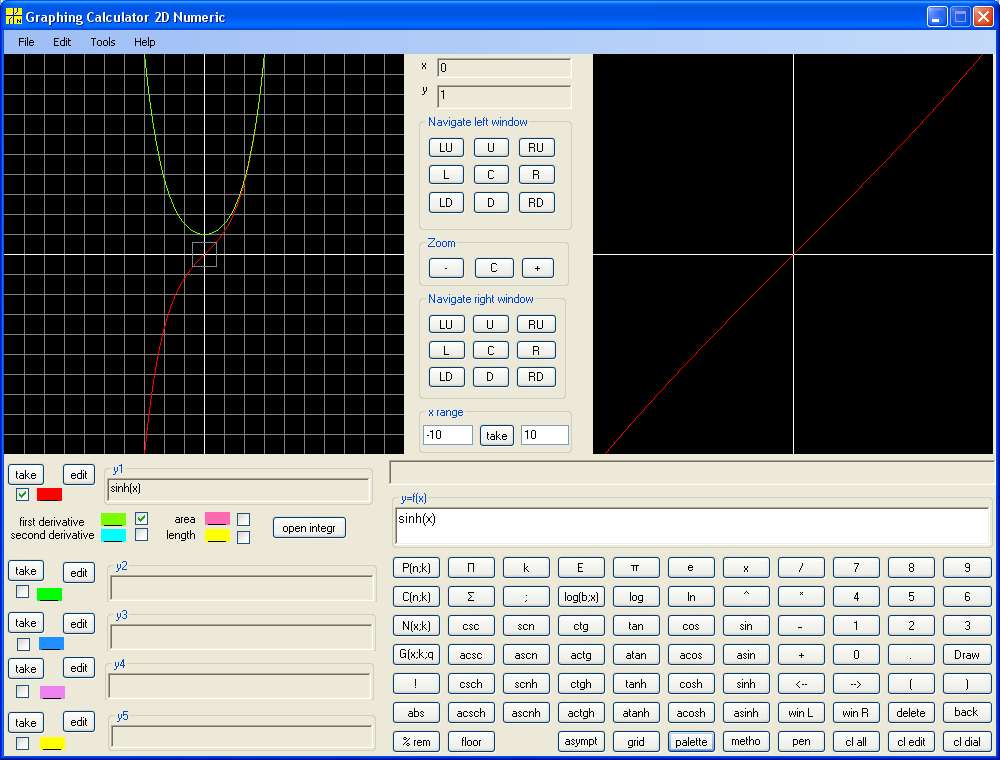
We see that the graph of first derivative (green graph) of sinh coincide with graph of cosh.

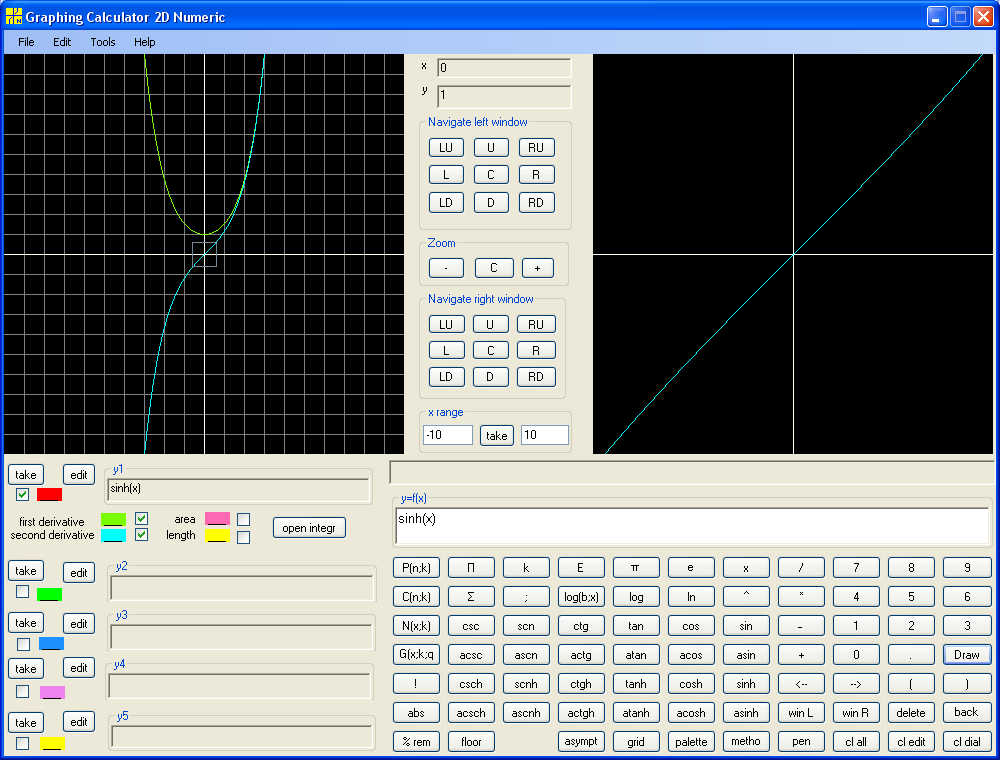
The graph of second derivative of sinh (light blue) coincides with the graph of sinh itself.

Similarly for y = cosh(x) :

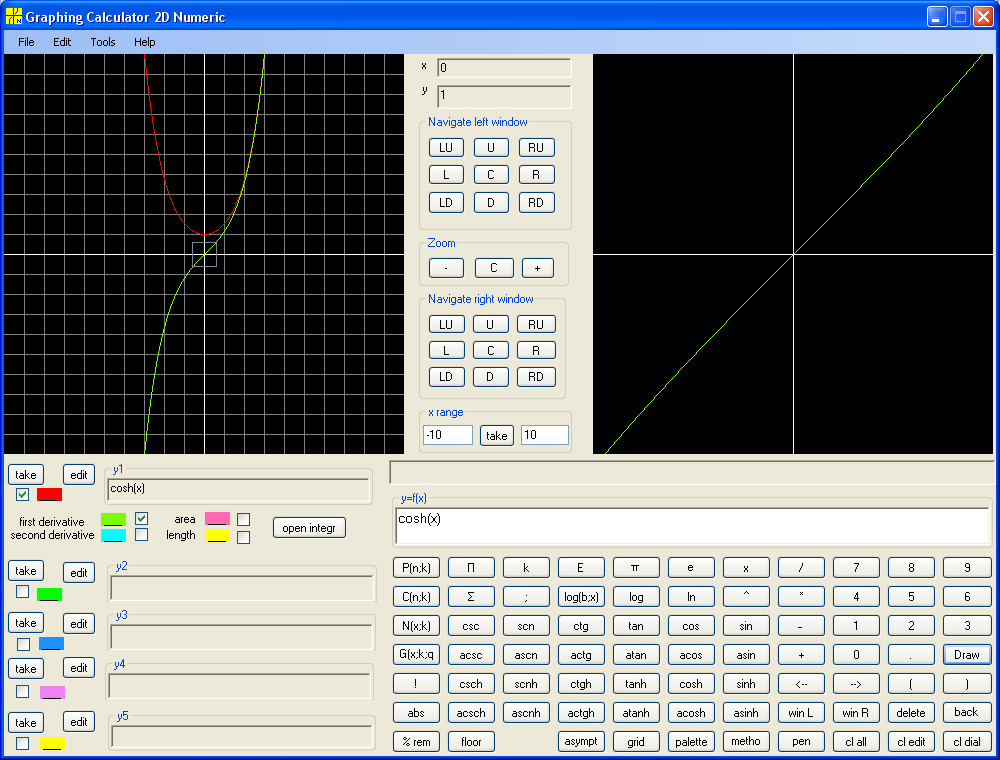
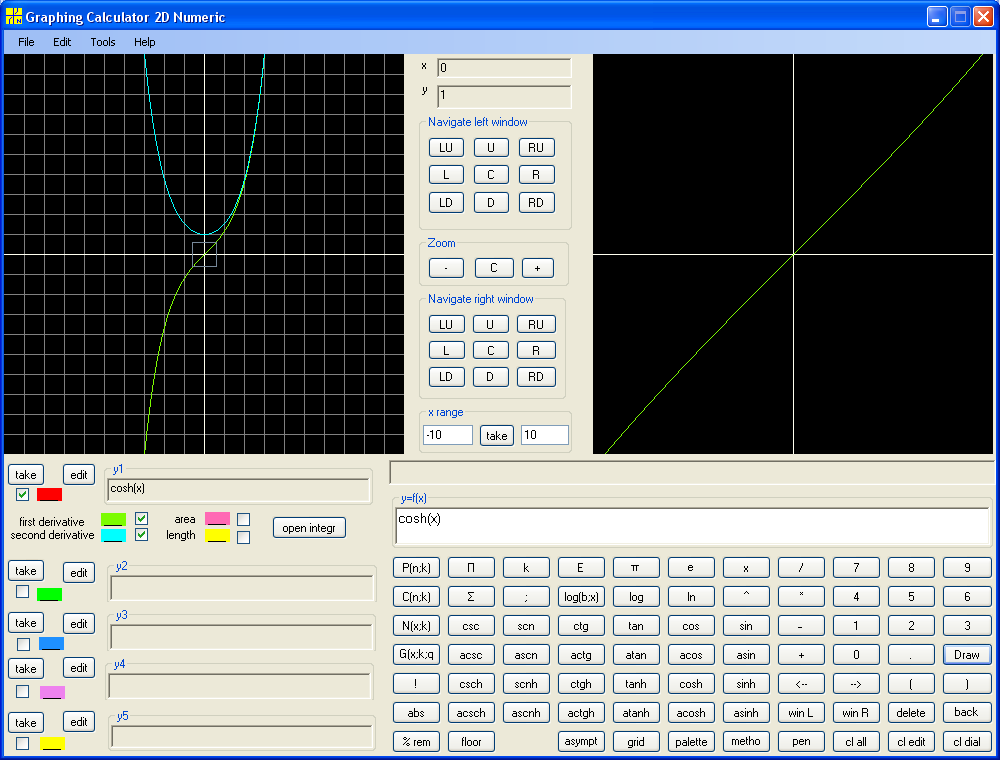
So, sinh' = cosh and cosh' = sinh. Recall sin' = cos and cos' = -sin .

Let's illustrate some identities.

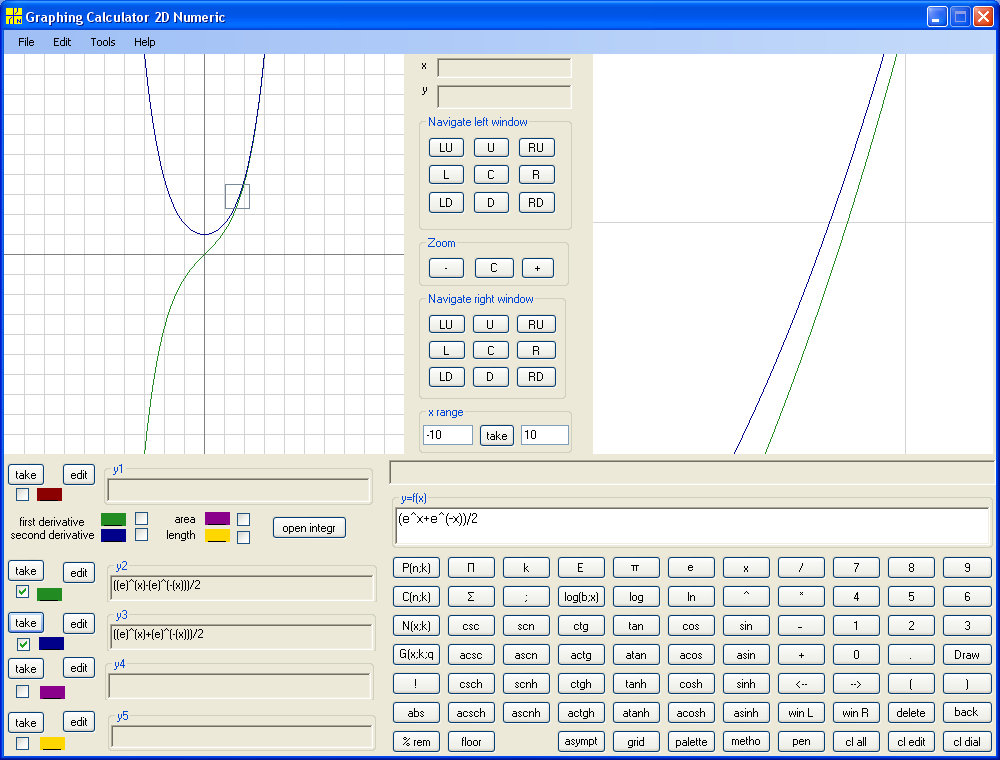
sinh(x) = (e^x - e^-x)/2 and   cosh = (e^x + e^-x)/2 :

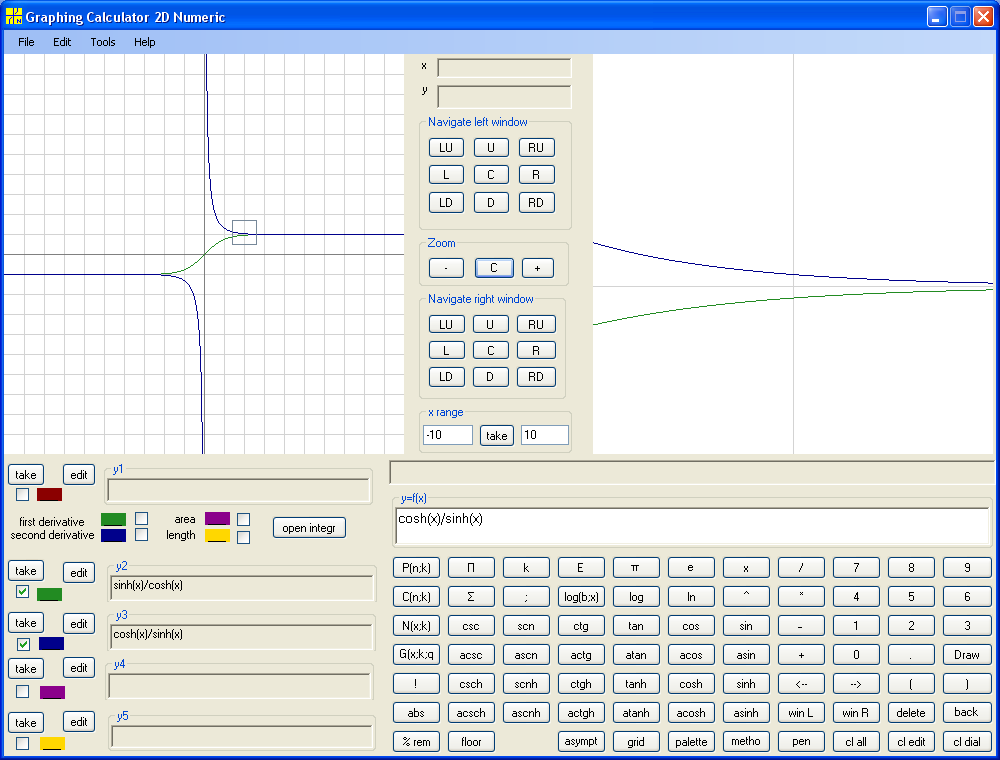
tanh(x) = sinh(x)/cosh(x)  and ctgh(x) =cosh(x)/sinh(x):

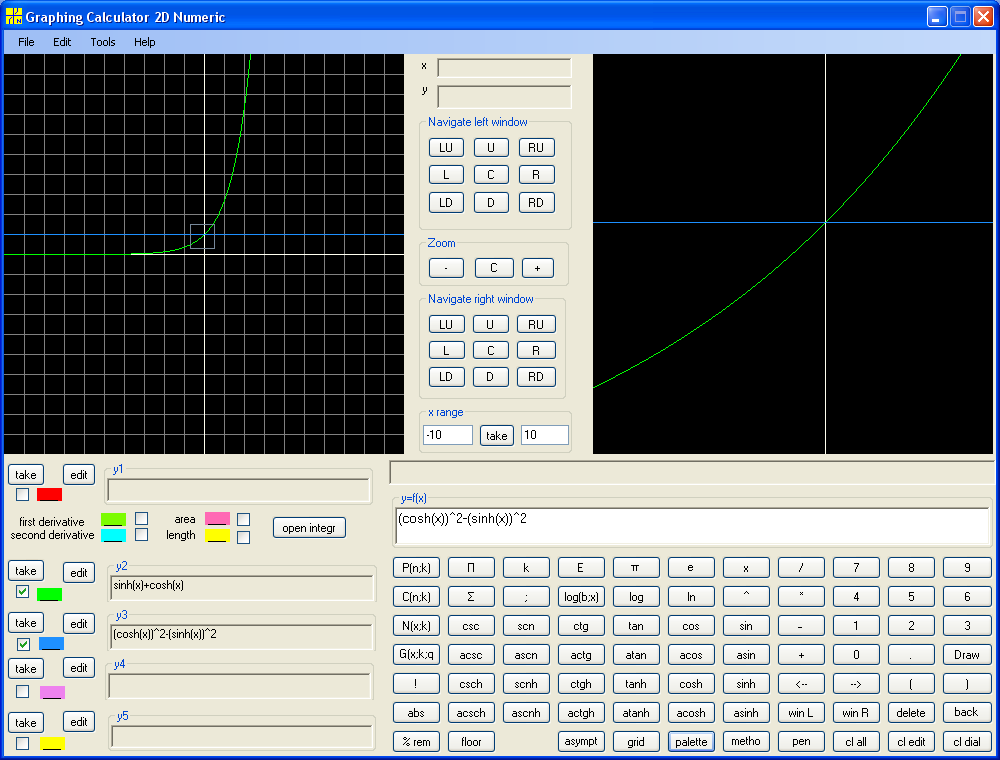
e^x = sinh(x) + cosh(x) and cosh²(x) - sinh²(x) = 1

It's time to explore inverse hyperbolic functions. Read first "Exploring Inverse Functions", if you haven't.

Similarly to trigonometric functions, there are a few different notations for inverse hyperbolic functions:  Arcsinh, arcsinh, asinh, sinh^-1, Arccosh, arccosh, acosh, cosh^-1, Arctanh, arctanh, atanh, atngh, atanh^-1, Arcctg, arcctgh, actgh, ctgh^-1, Arcsech, arcsech, asech, ascnh, sech^-1, Arccsch, arccsch, acsch, scsh^-1 .

Consider y = asinh(x) :

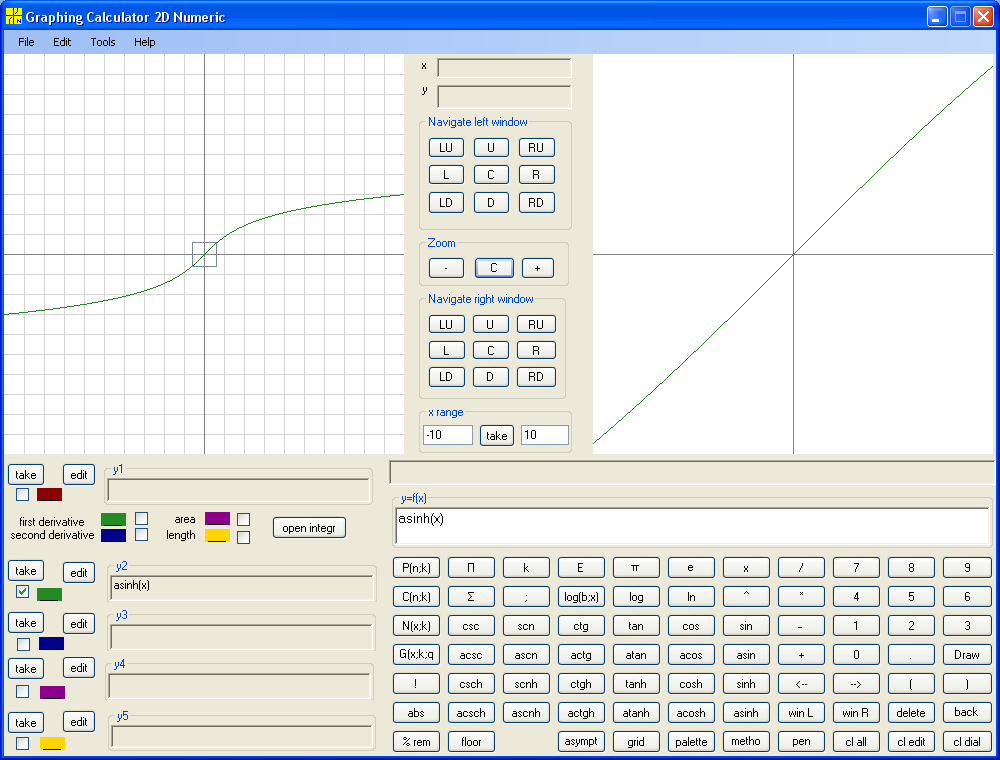
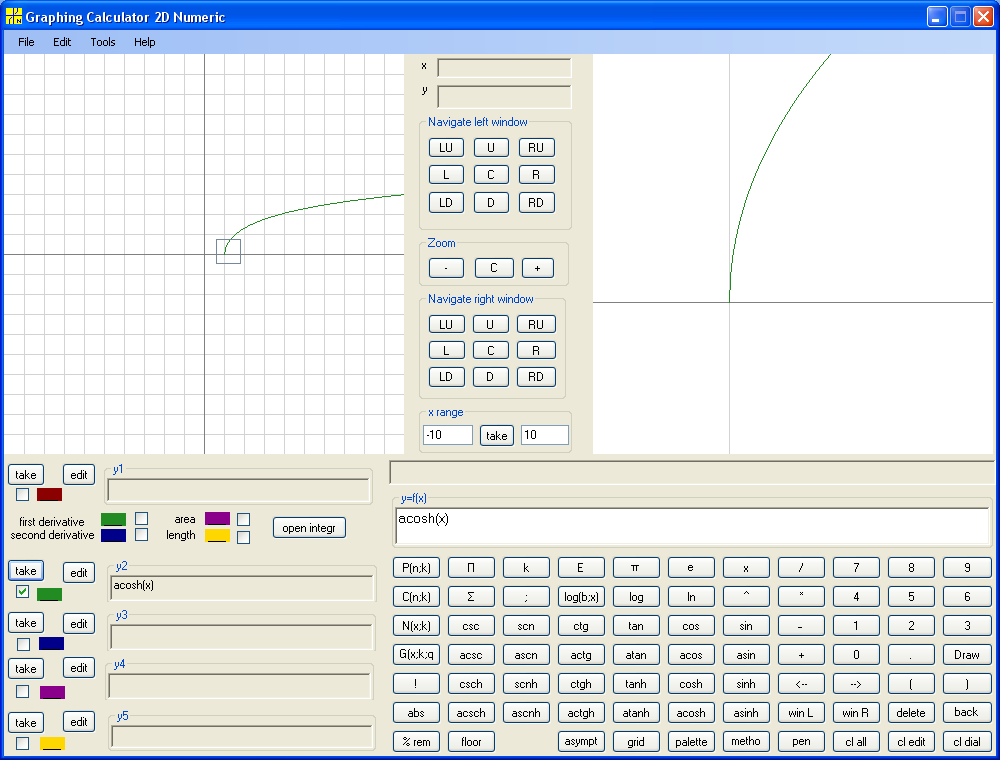
y = acosh(x) :

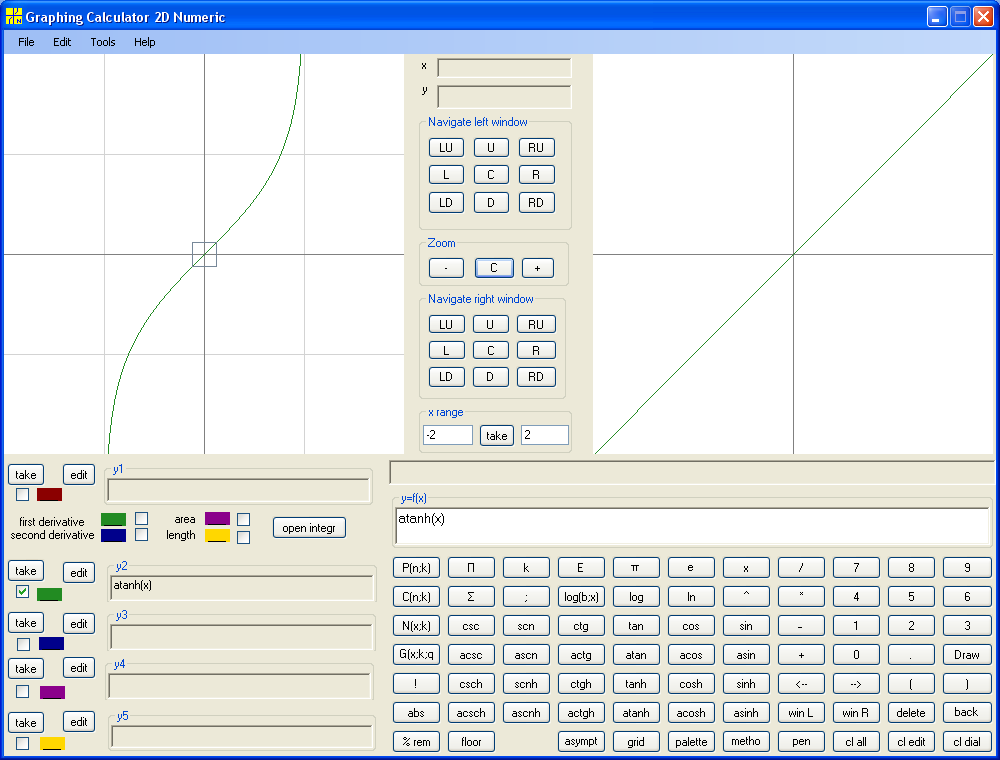
y = atanh(x) :

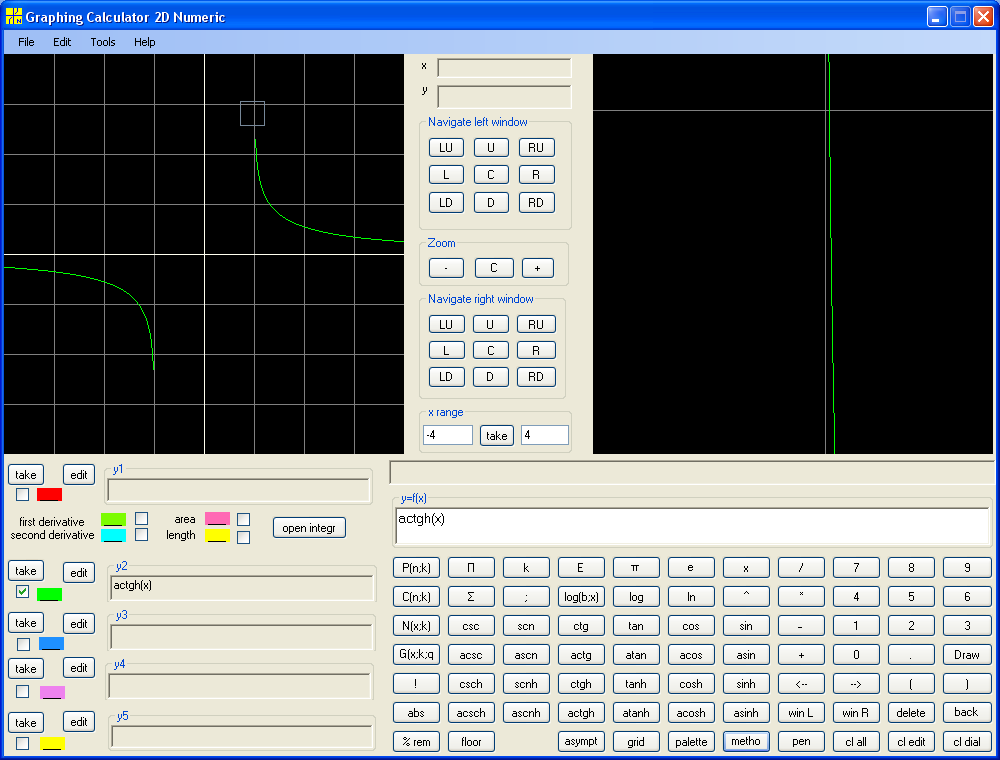
y = actgh(x) :

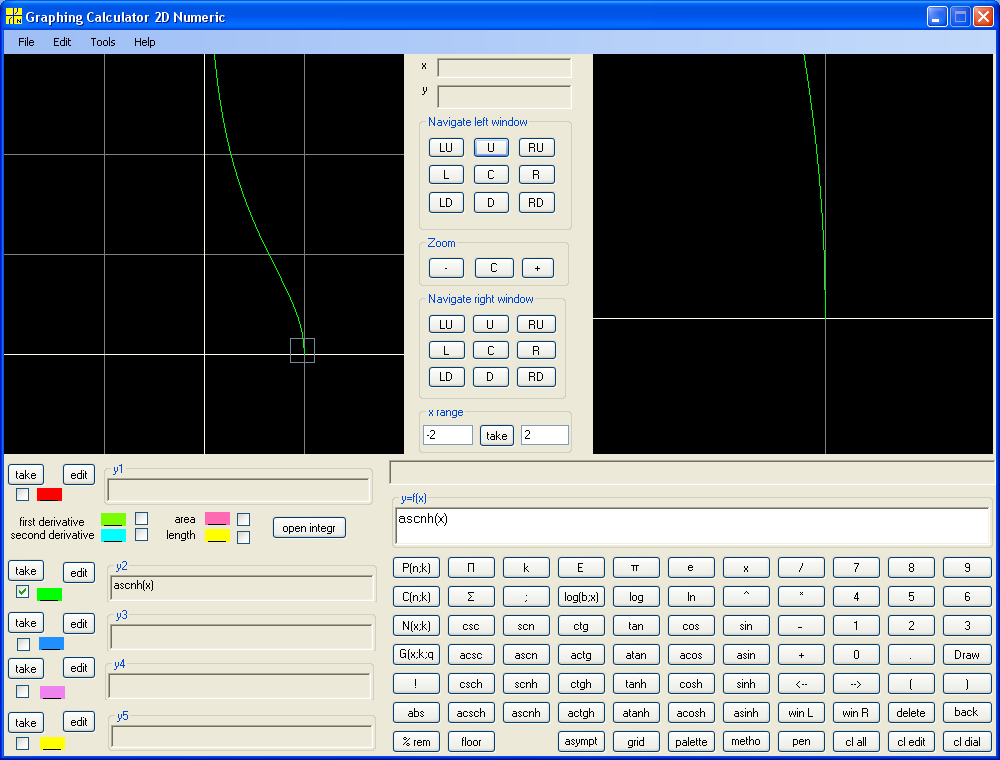
y = ascnh(x) :

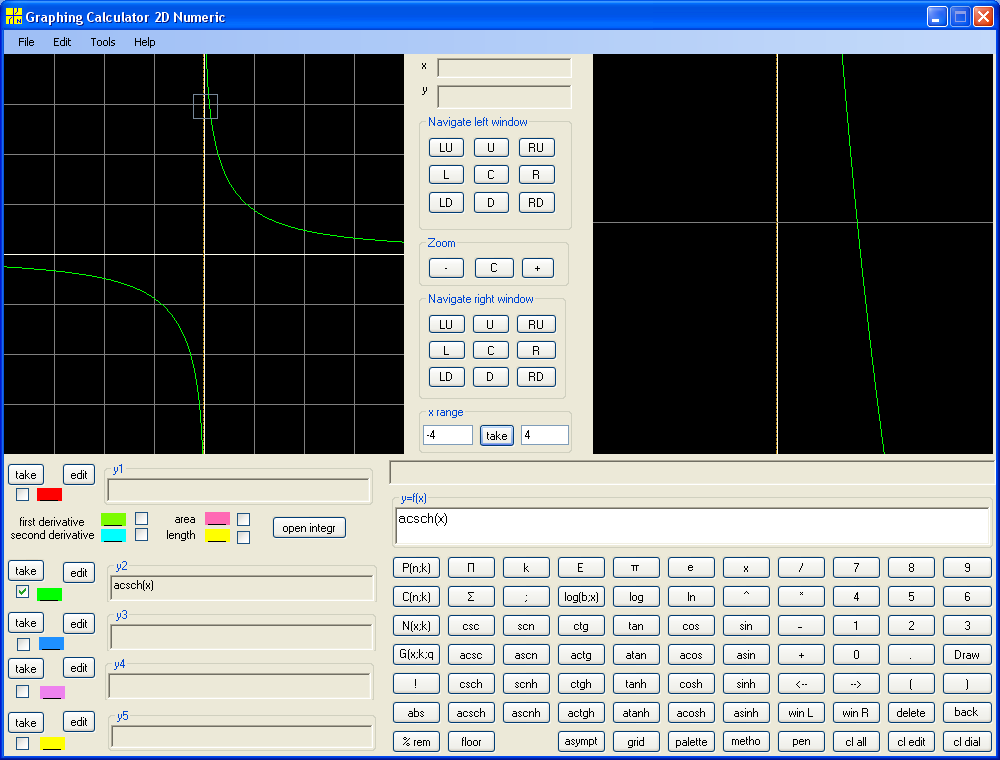
y = acsch(x) :

© 2008 Tvalx