Mathematical Software. Mathematical Research. Mathematical Education. Tvalx Products.
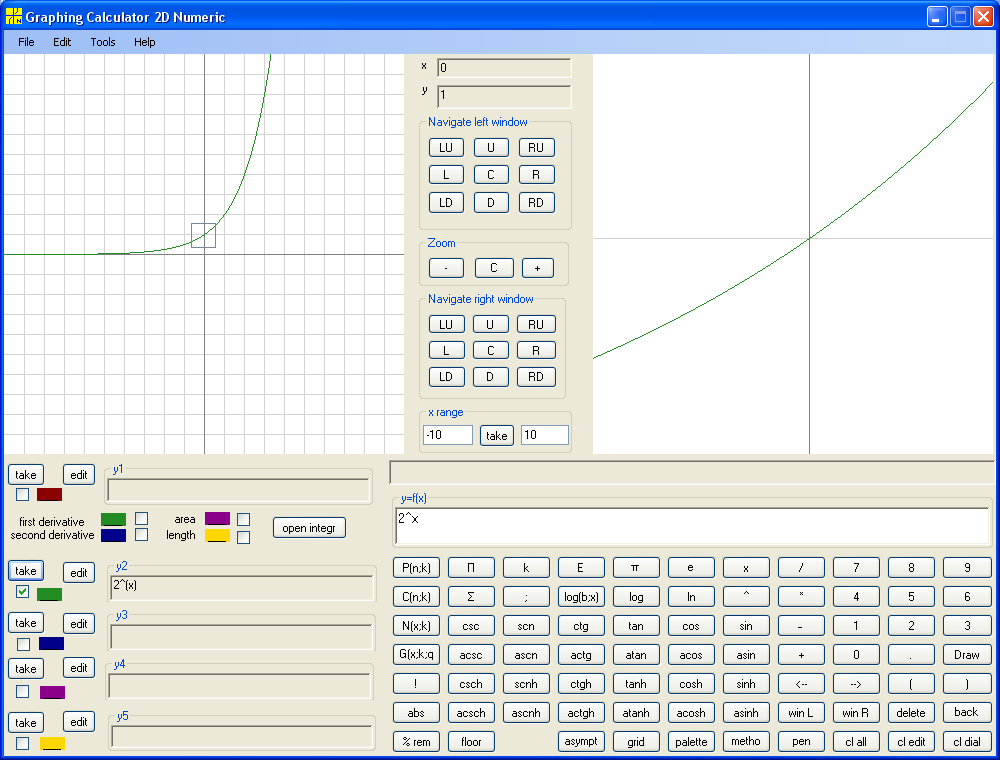
There is no short formal definition of inverse functions. Here we try to avoid formal definition and describe inverse functions in order to introduce reader to the concept. Let's consider function y = 2^x, using superscript y = 2x :

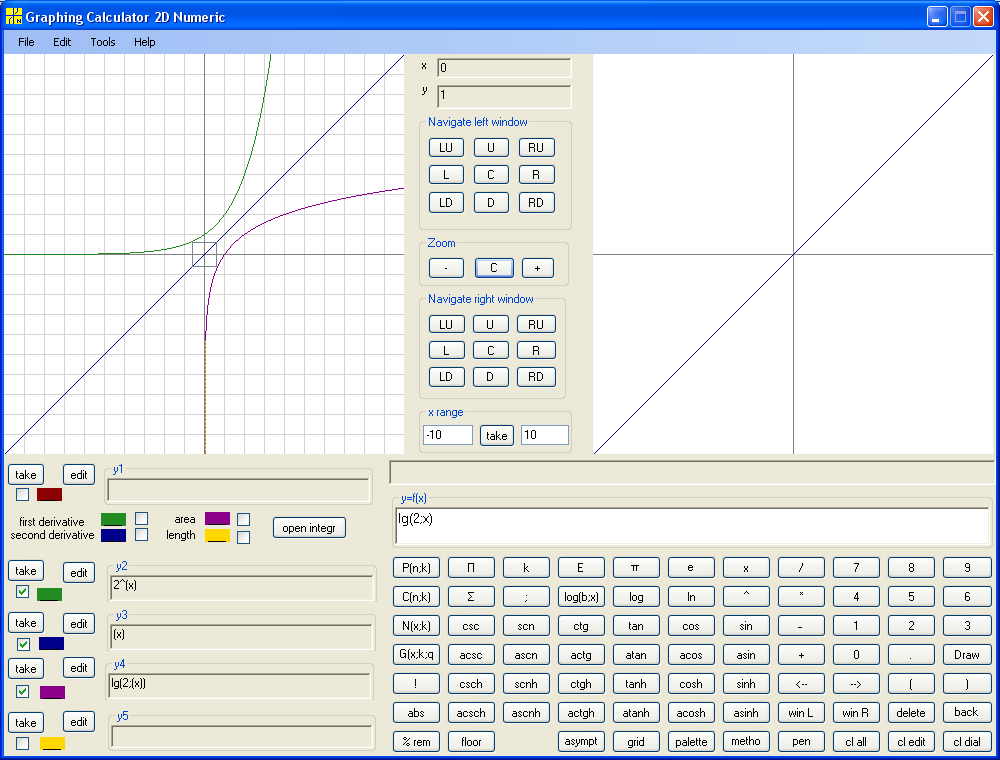
When x=0, y=2^0=1. When x=1, y=2^1=2. When x=2, y=2^2=4. Now lets' ask: for what x y=1? Answer: for x=0. For what x y=2? For x=1. For what x y=4? For x=2. Thus for any given value of y we have corresponding exactly one x. This satisfies the definition of function. So, we have a function where y is argument and x is a value and where the domain is range of y=2^x and range is domain of y=2^x. By construction our function for given argument a returns real number b such that a=2^b. This is a definition of logarithm with base 2. Notation b=log2a or x=log2y . Since by convention argument is denoted by x and value by y, we have to switch x and y. Thus we get y=log2x. This function is by construction the inverse function of y = 2x. Note that graph for y = 2x and graph for x=log2y coincide. But when we switch roles of x and y, the graph is reflected with respect to the main diagonal of coordinate system. Thus graph of y=log2x is symmetric to graph of y = 2x with respect to the main diagonal :
Now consider y=sin(x). Let's build an inverse function for Sine. So, for given value of y we want to find x such that y=sin(x). Let's denote such inverse function by g. So, x=g(y). Now switch roles of x and y. We get y=g(x). We now that graph of y=g(x) symmetric to graph of y=sin(x) with respect to the main diagonal. We can build such picture using Graphing Calculator 2D Parametric from Math Center Level 2 :
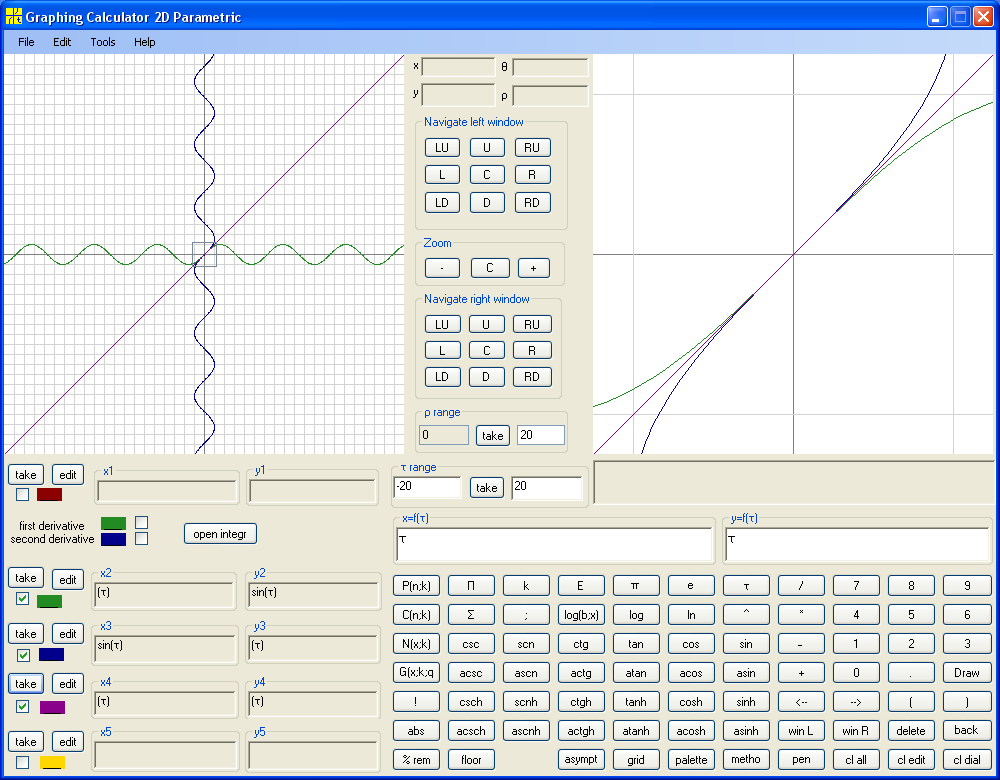
We see that the graph of g(x) does not satisfy requirement for functions that for given x there is exactly one corresponding y. So, what we built is not a function. Where things went wrong? The difference between y = 2x and y=sin(x) is that the first is one-to-one function and the second is not. We cannot build inverse function for y=sin(x) on the same way as for y = 2x . The remedy of the situation is to narrow domain of sin(x) to size where it is on-to-one. We can choose any interval of length π but convention is to choose near the origin, from -π/2 to π/2 . On such domain sin(x) is one-to-one. Now we can build inverse function g(x) for such "limited" sin(x) :
![y=sin(x) and y=asin(x) on [-pi/2, pi/2]](GraphingCalculator2DParametricInverseSine02.png)
The green line is graph of narrowed Sine and the blue line is inverse function of Sine. In the right window we can see that near origin both functions are close to main diagonal y=x. Historically the inverse function of Sine was called Arcsine, that is arc (angle) corresponding to given value of Sine. The domain of Arcsine is interval [-1, 1] and the range is [-π/2, π/2] .
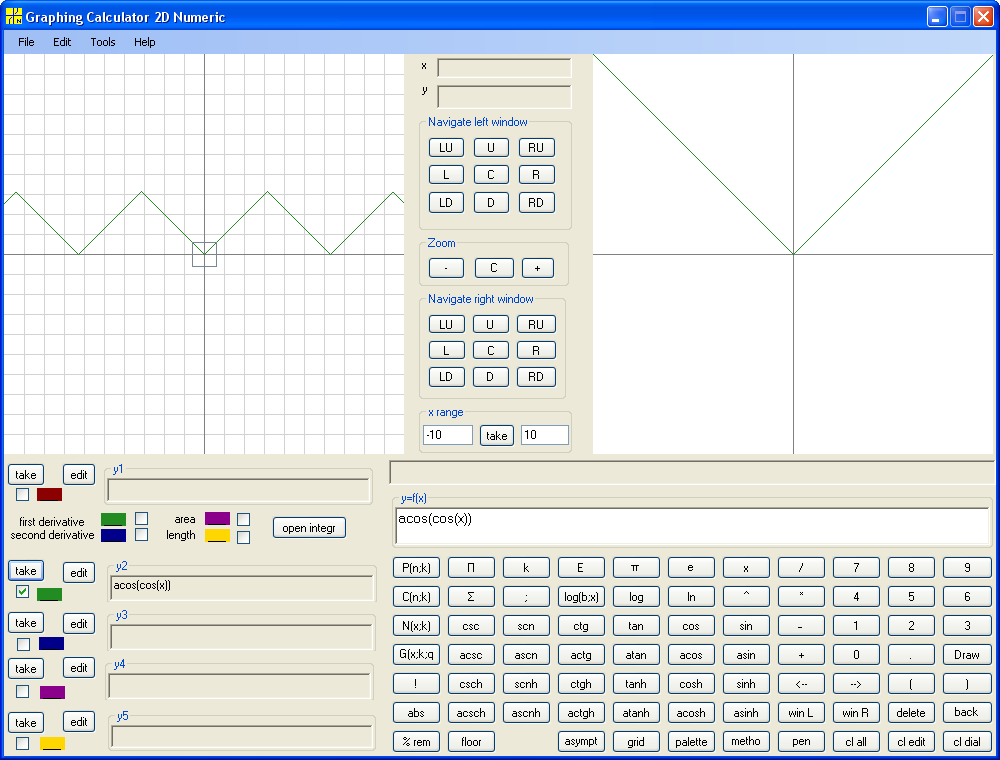
Similarly we build Arccosine for Cosine with domain [-1, 1] and range [0, π] . The purple line is graph of Cosine and the yellow line is graph of Arccosine .
![y=cos(x) and y=acos(x) on [0, pi]](GraphingCalculator2DParametricInverseCosine.png)
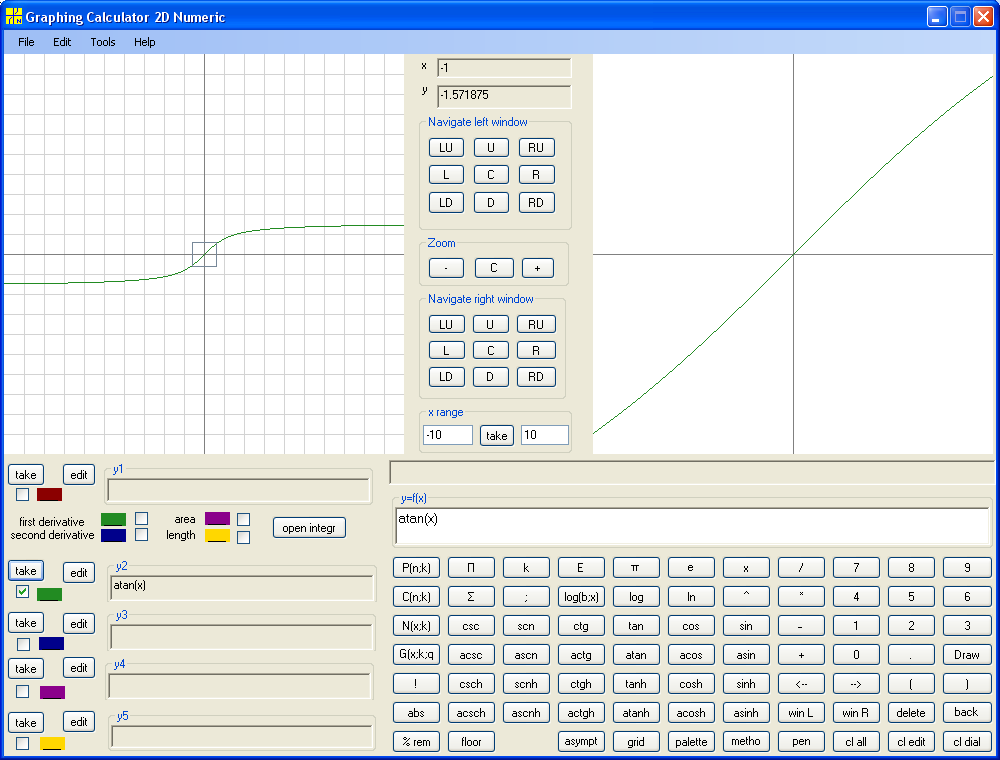
Similarly we build Arctangent with domain the entire real line and range (-π/2, π/2) .
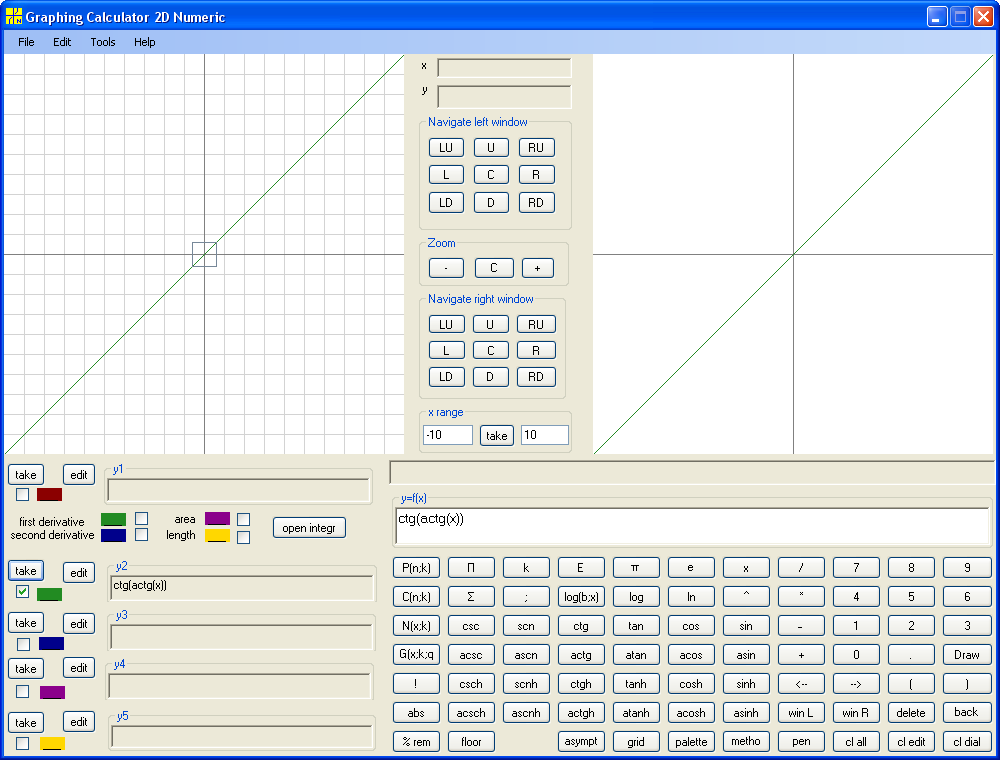
Similarly we build Arccotangent with domain consisting of two intervals (-infinity, 0), (0, infinity) and range consisting of two intervals [-π/2, 0), (0,π/2] . Note that zero is not in the range. Indeed, at arc zero Sine is zero. Since ctg(x)=cos(x)/sin(x), ctg(0) would be cos(0)/sin(0)=1/0 what is impossible. The green graph of Arccotangent is a reflection of central part of blue graph of Cotangent with respect to main diagonal. Although left (coarse) window shows green vertical line (limitation of programming) the right (finer) window shows that Arccotangent is not define at zero.
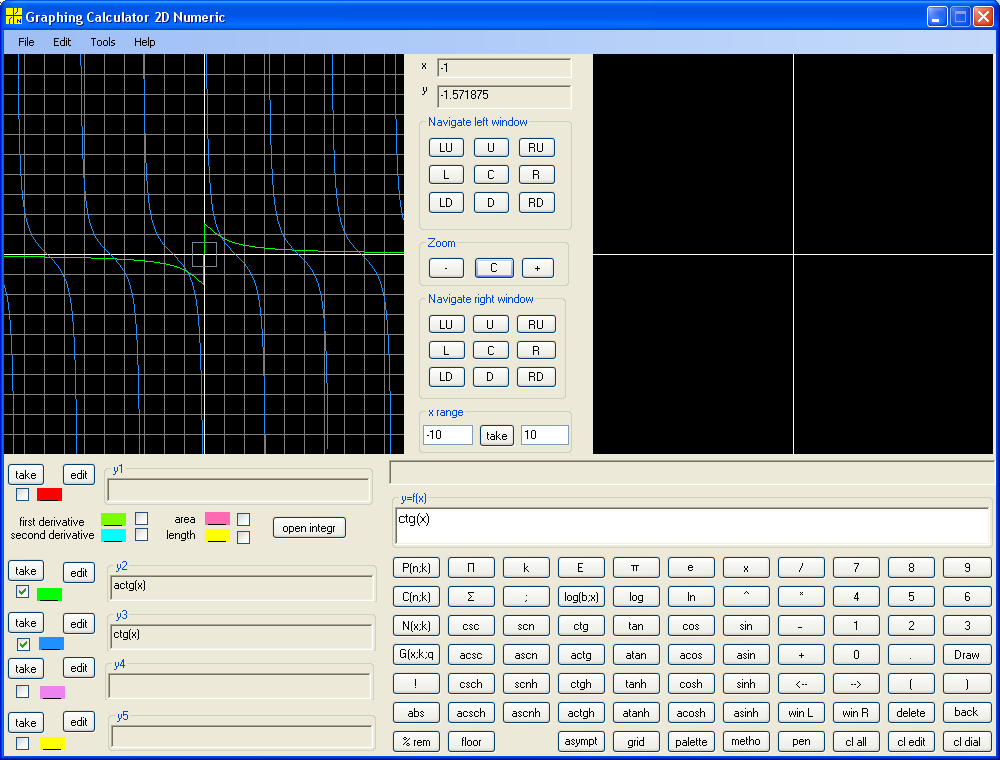
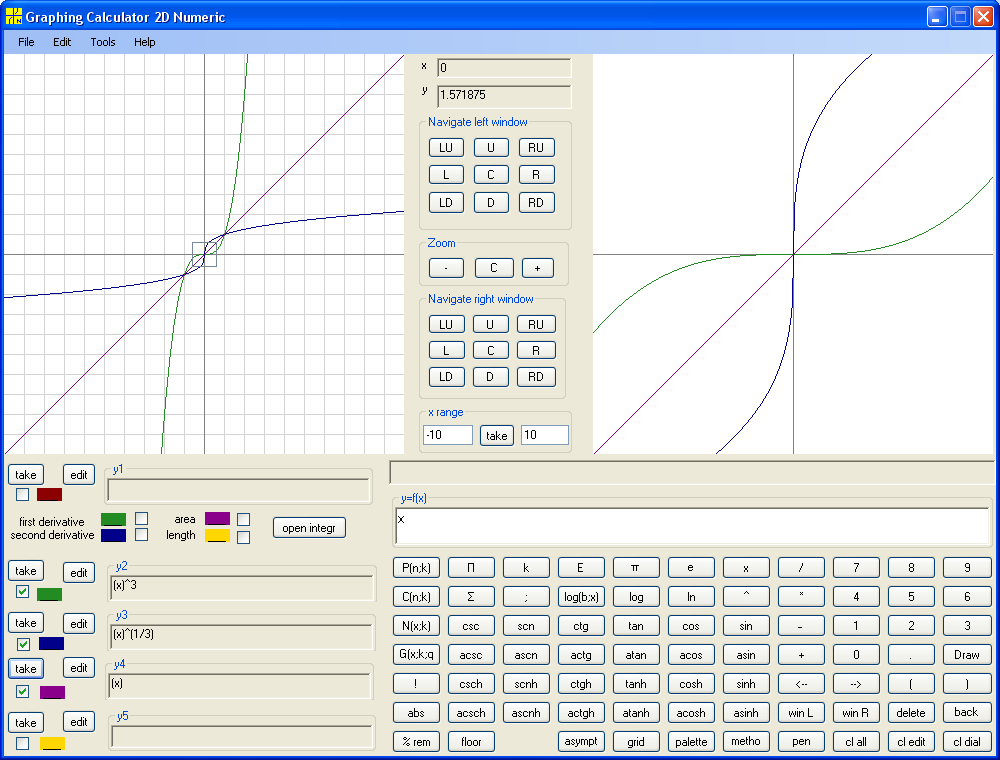
After building inverse trigonometric functions the task of building inverse function of y=x^3 is easy. Obviously this is third root of x, or the same y=x^(1/3):
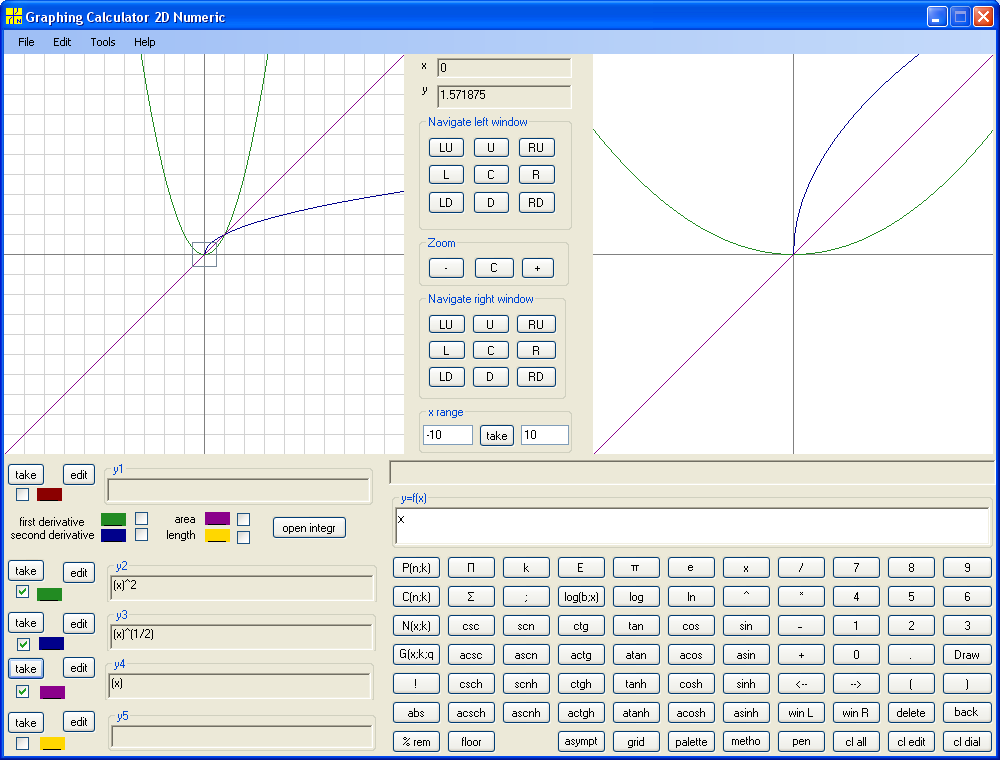
Consider y=x^2. Again this is not one-to-one function and we narrow domain of y=x^2 to interval [0, infinity), where y=x^2 is one-to-one. Obviously the inverse function of y=x^2 is square root of x, y=x^(1/2) :
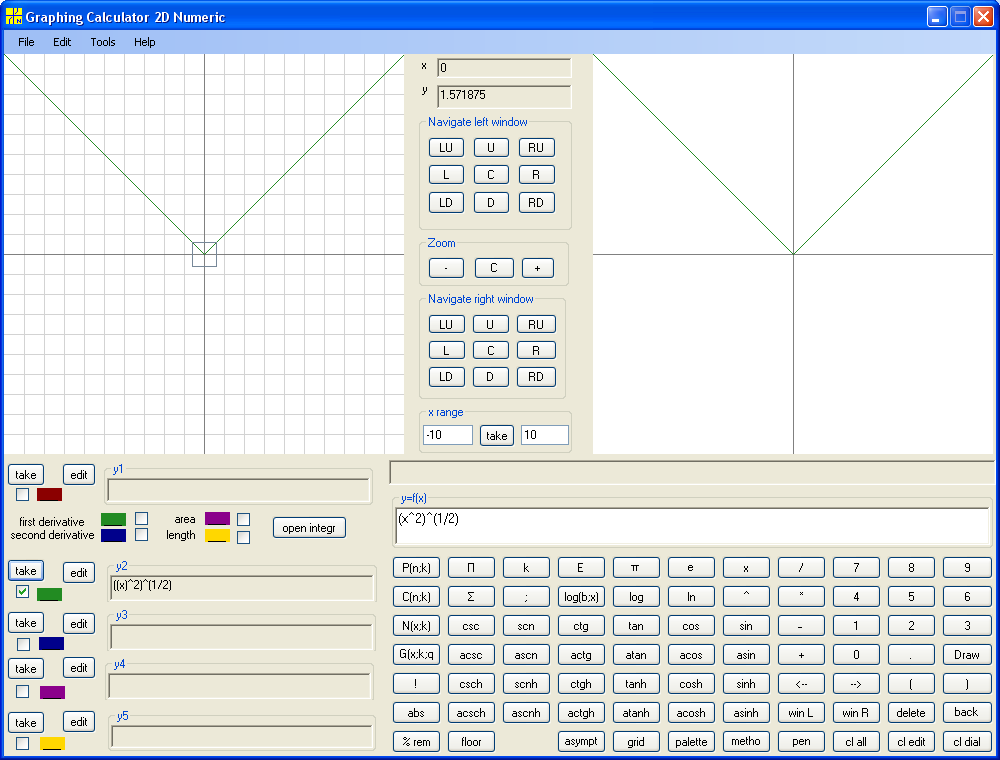
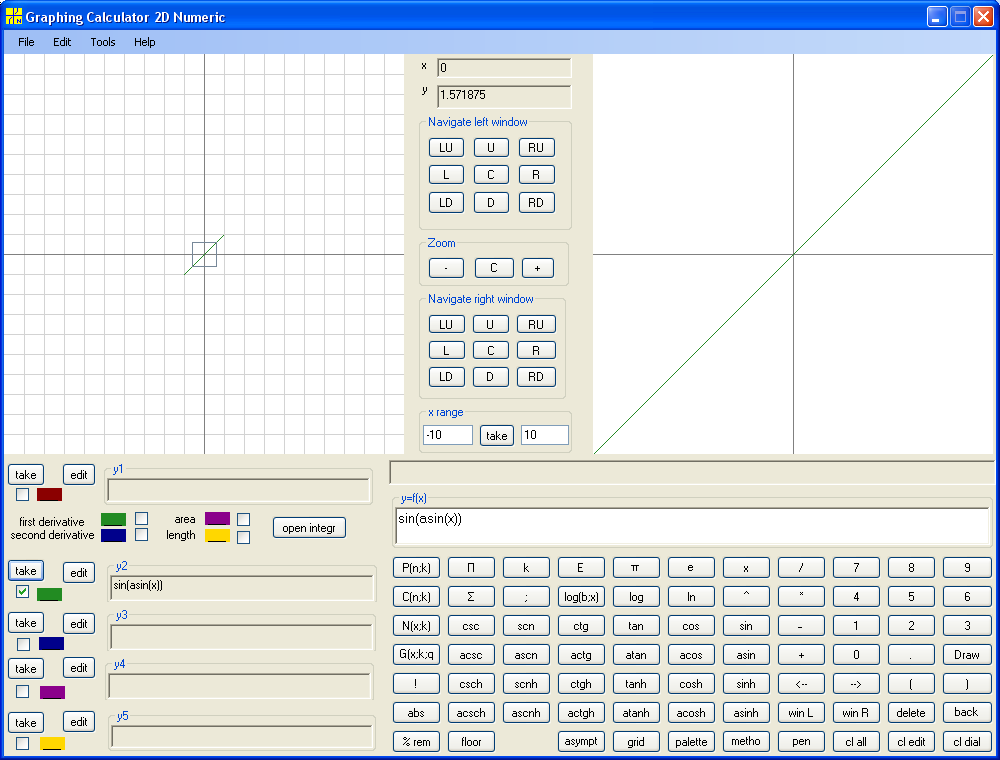
Note that we learn to build inverse function for any function. We map functions to functions similarly to mapping numbers to numbers. The mapping of functions to functions is called operator. So we apply inverse function operator to a function f(x) and get inverse function g(x). Such g(x) is denoted f -1(x). Looks similar to f(x) in power minus one. Use context to distinguish. Thus instead of Arcsine, Arccosine, Arctangent and Arccotangent we can write sin-1, cos-1, tan-1, ctg-1 . Note that inverse function of inverse function is the original function, that is (f -1(x))-1=f(x) . Also note that f(f -1(x))=x on domain of f -1(x) but f -1(f(x)) is not necessarily x on domain of f(x). What is the trick? The difference is in domain (and range). The domain of f(f -1(x)) is domain of f -1(x), that is range of f(x), and domain of f -1(f(x)) is domain of f(x). The graph of f(f -1(x)) is always a part of the main diagonal. The graph of f -1(f(x)) may coincide with main diagonal only at the origin (sometimes with entire main diagonal). Below are examples.
y=(x^2)^(1/2)
y=(x^(1/2))^2
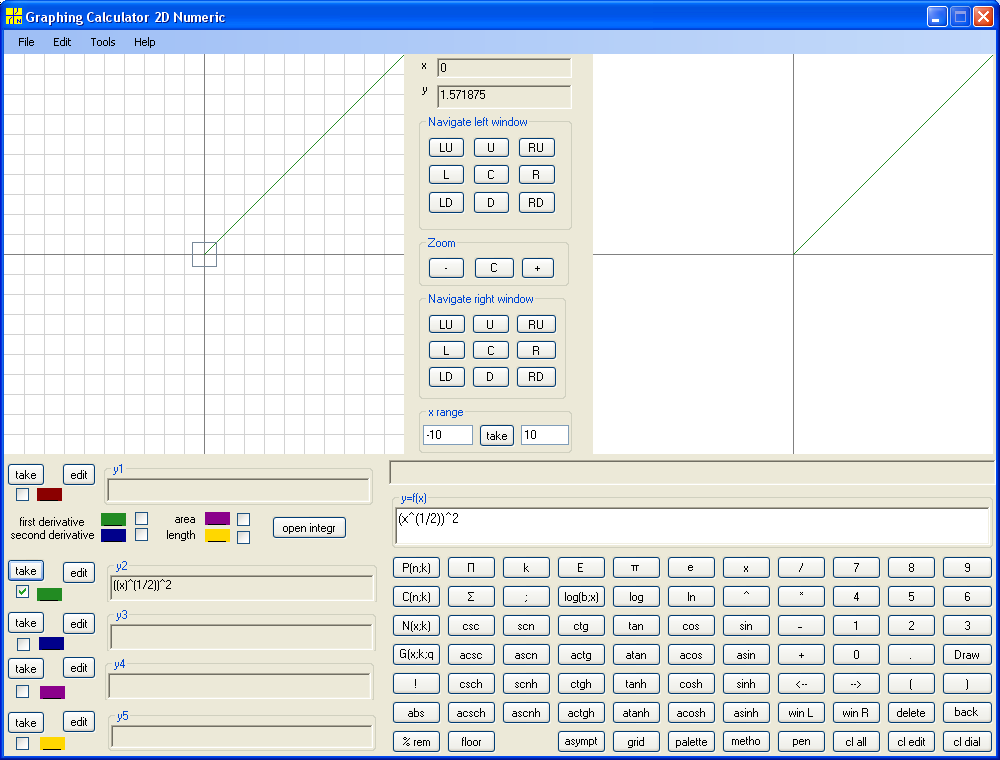
y=arcsin(sin(x))
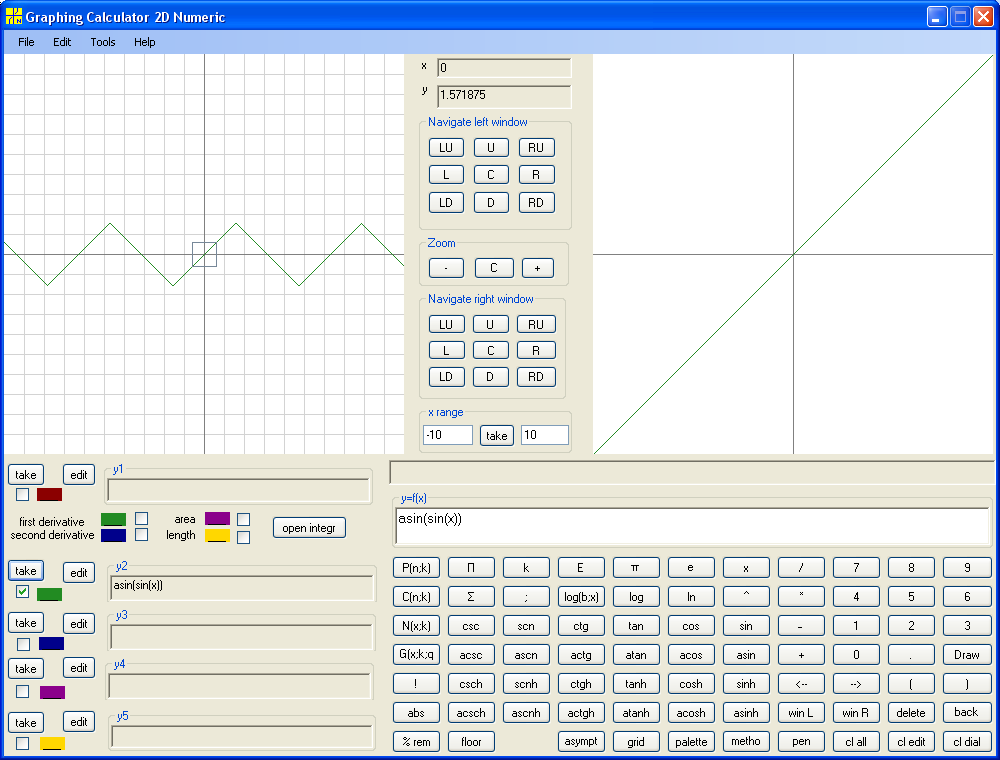
The same graph as arcsin(sin(x)) has function (-1)^floor(1/2 - x/π)*(x+π*floor(1/2-x/π)) .
y=sin(arcsin(x))
y=arccos(cos(x))
y=cos(arccos(x))
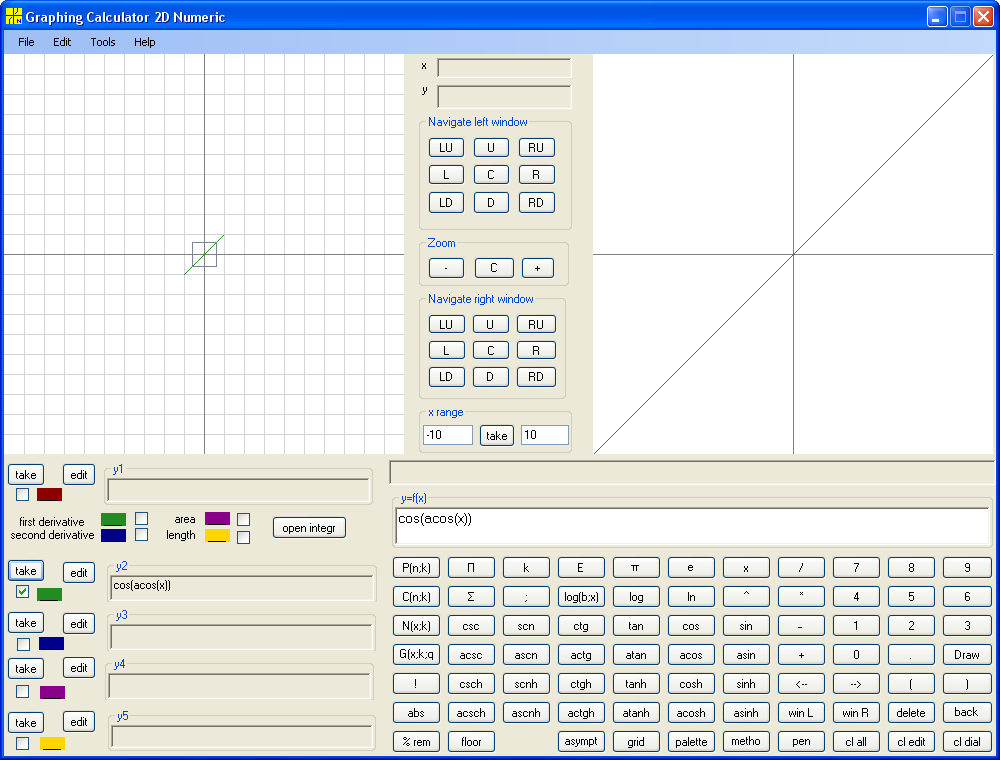
y=arctan(tan(x))
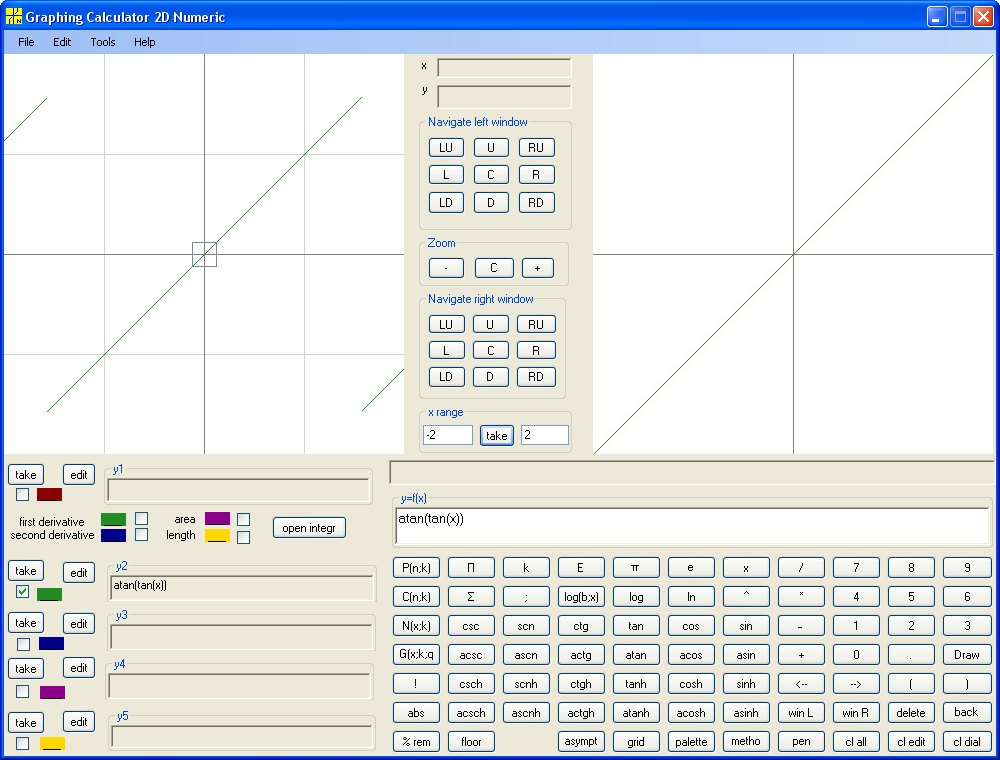
y=tan(arctan(x))
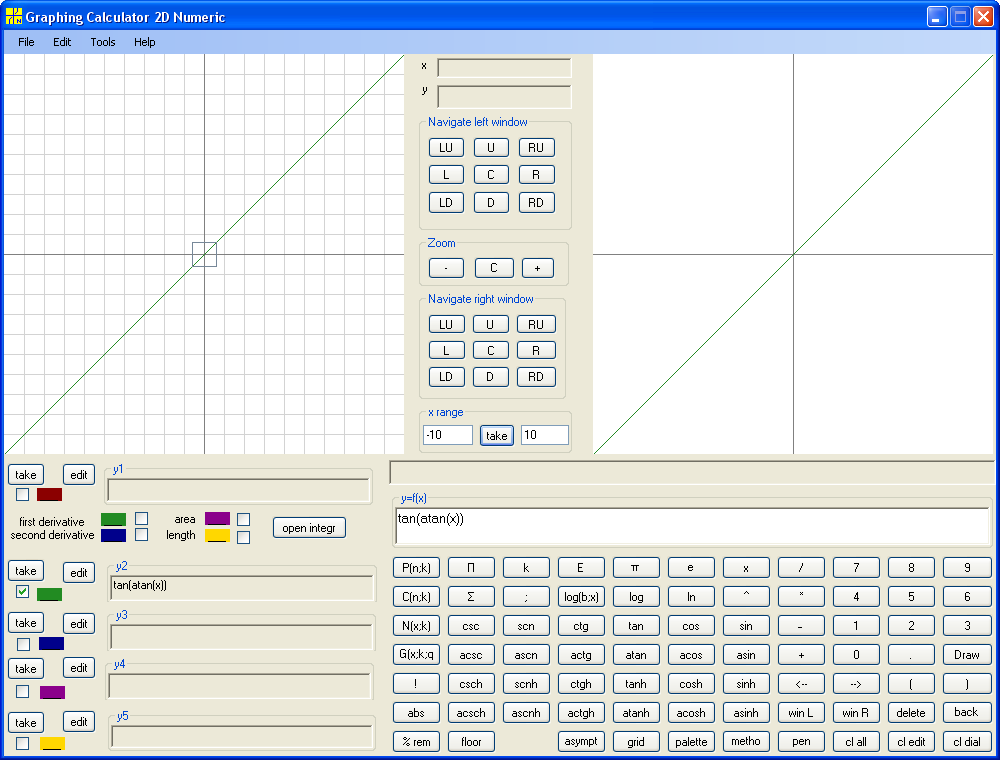
y=arcctg(ctg(x))
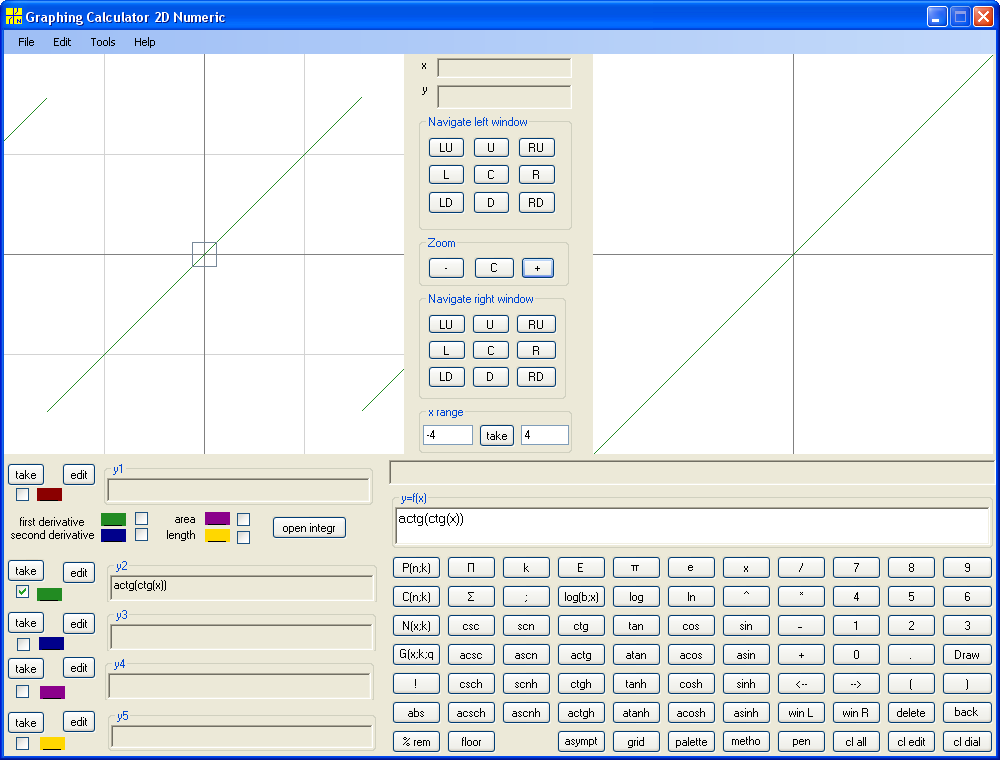
y=ctg(arcctg(x))
© 2008 Tvalx
