Exploring Taylor and Maclaurin Polynomials
Mathematical Software. Mathematical Research. Mathematical Education. Tvalx Products.
As we know, internal computer operations are pretty primitive binary
operations. We cannot expect that there are machine codes for computing
expressions like sin(1/4). It's a tasks for programmer. Of course, Maclaurin and
Taylor polynomial should be involved here as bridge between arithmetic
operations and smooth functions. Let's explore capabilities of Maclaurin and
Taylor series with help of Graphing Calculator 2D Numeric from
Math Center Level 2 .
Consider graph of Sine y=sin(x). Maclaurin series for Sine is
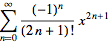 .
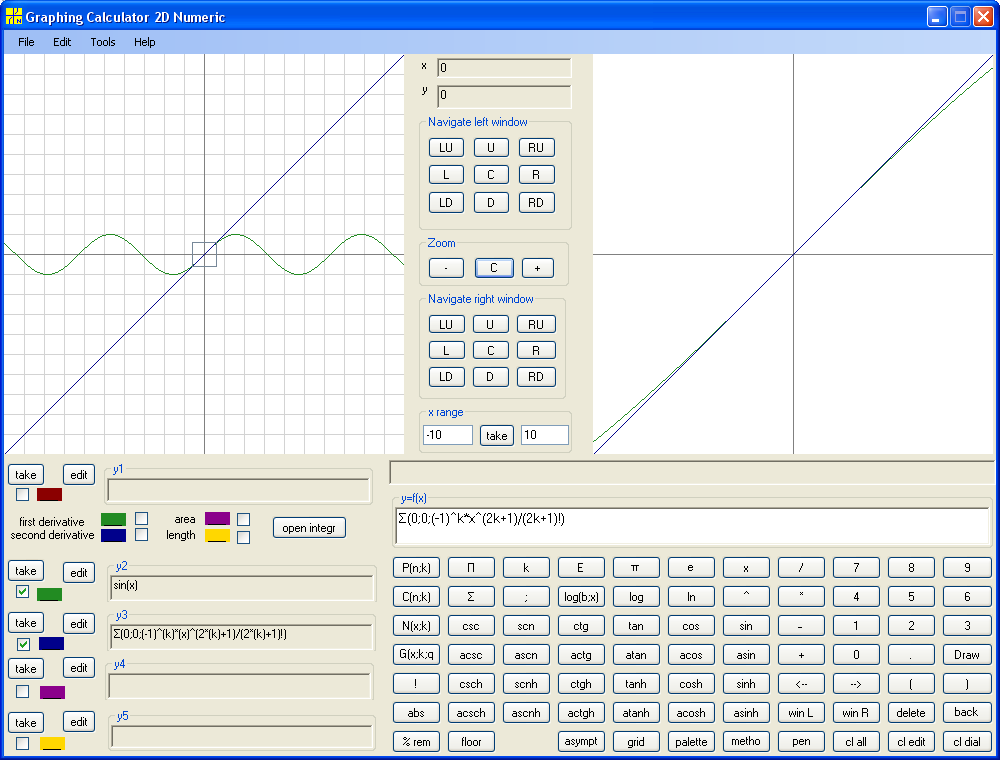
Let's compare graph of Sine with graphs of Maclaurin polynomials of different
degree for Sine. In terms of Graphing
Calculator 2D Numeric the Maclauren polynomial for Sine is Σ(0; degree;
(-1)^k*x^(2k+1)/(2k+1)!) . Even the polynomial of zero degree, that is y=x, is a
good approximation near the origin .
.
Let's compare graph of Sine with graphs of Maclaurin polynomials of different
degree for Sine. In terms of Graphing
Calculator 2D Numeric the Maclauren polynomial for Sine is Σ(0; degree;
(-1)^k*x^(2k+1)/(2k+1)!) . Even the polynomial of zero degree, that is y=x, is a
good approximation near the origin .
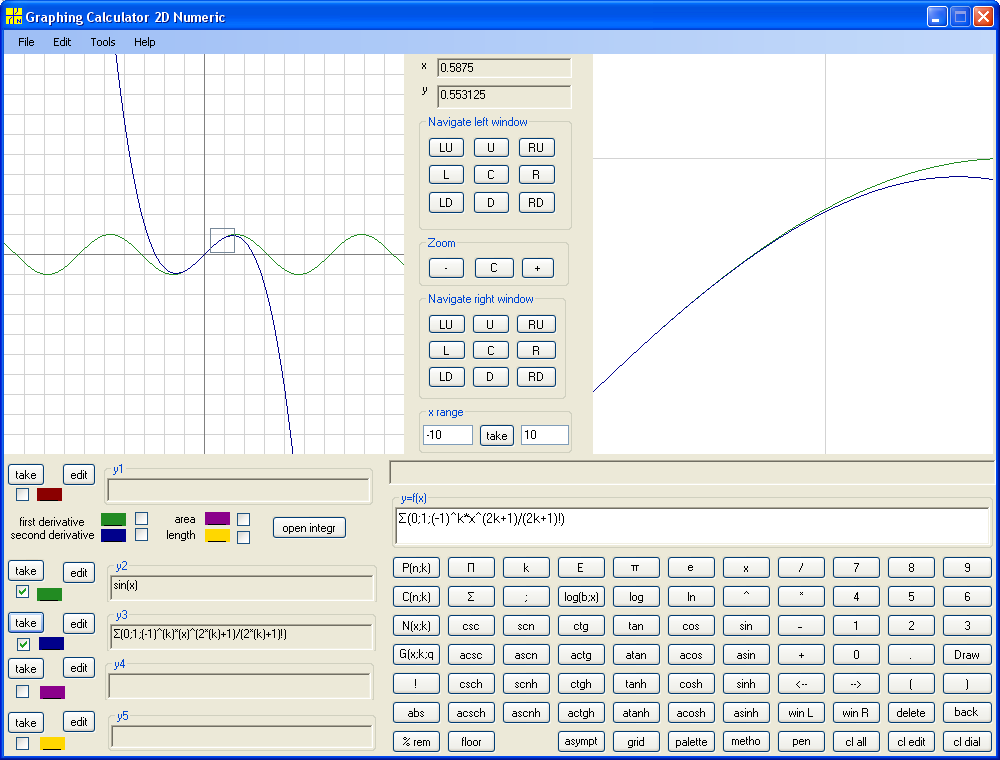
Next is the Maclaurin polynomial of first degree :
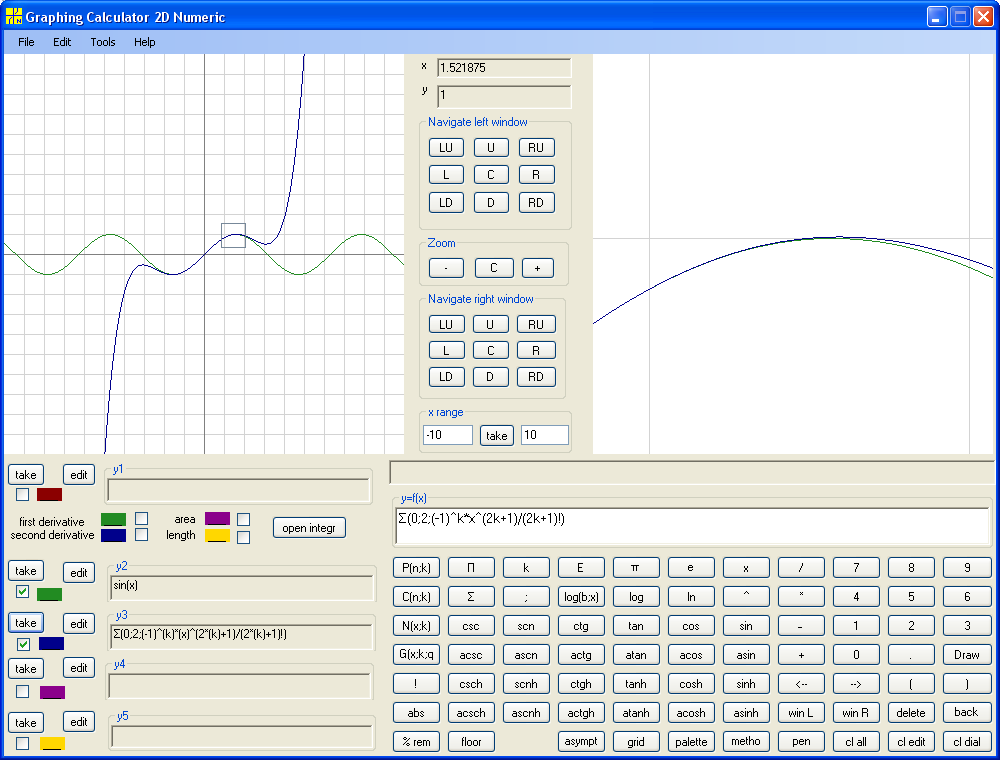
Next is the Maclaurin polynomial of second degree :
Next is the Maclaurin polynomial of third degree :
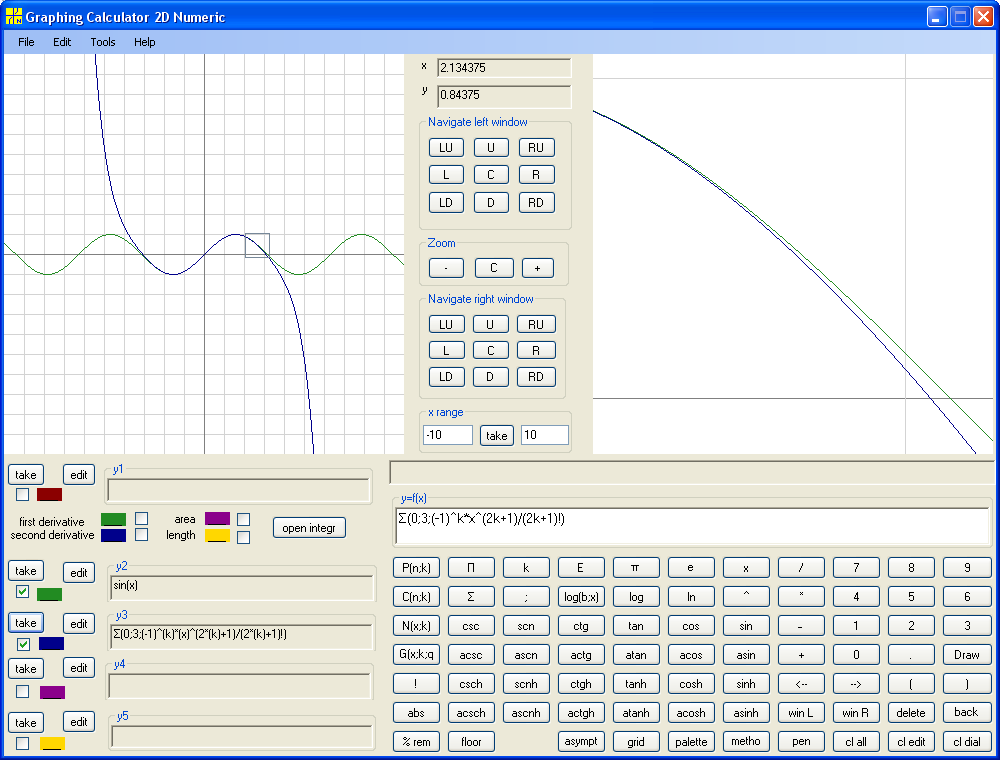
Next is the Maclaurin polynomial of fourth degree :
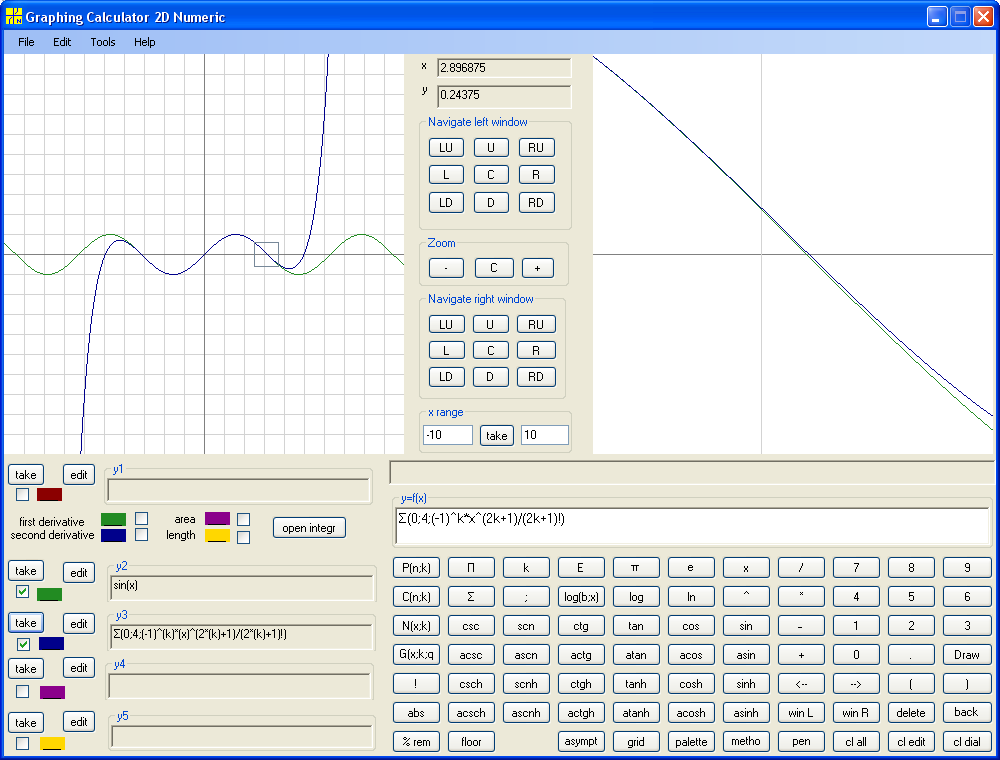
Now the general picuture becomes clear. Let's accelerate and jump to
Maclaurin polynomial of tenth degree :
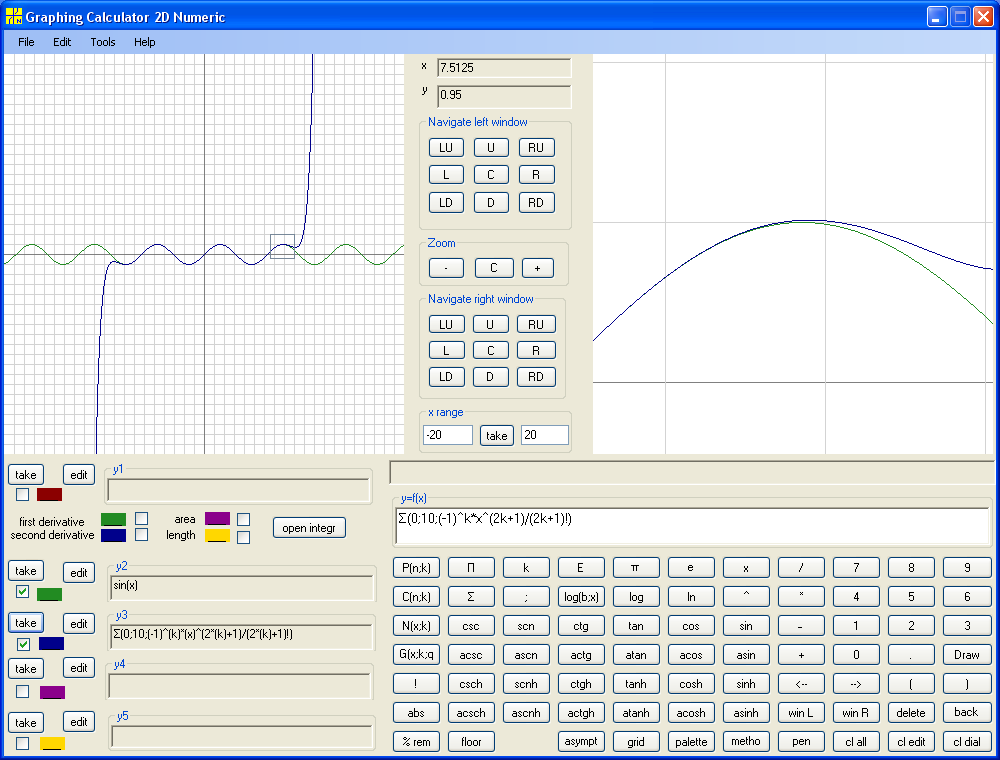
Next is the Maclaurin polynomial of twentieth degree :
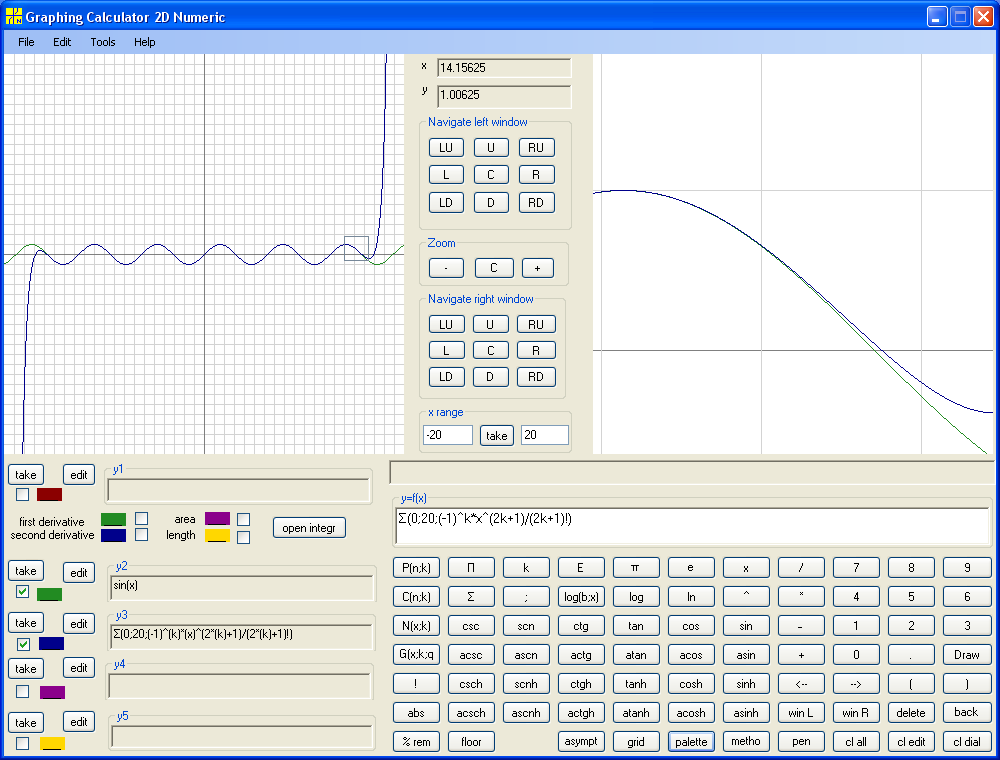
It is clear that we can find Maclaurin polynomial of sufficiently big degree
for any x. Thus we can approximate sin(x) on interval of any length around the
origin calculating Maclaurin polynomial of sufficiently big degree . Sounds good
except that calculation of Maclaurin polynomial of twentieth degree was notably
longer than calculation of Maclaurin polynomial of fourth degree. We know that
adding a number n to x in formula of function shifts graph to the left by n
units. Correspondingly subtracting a number n to x in formula of function
shifts graph to the right by n units . Lets try Σ(0;4;(-1)^k*(x-5)^(2k+1)/(2k+1)!) :
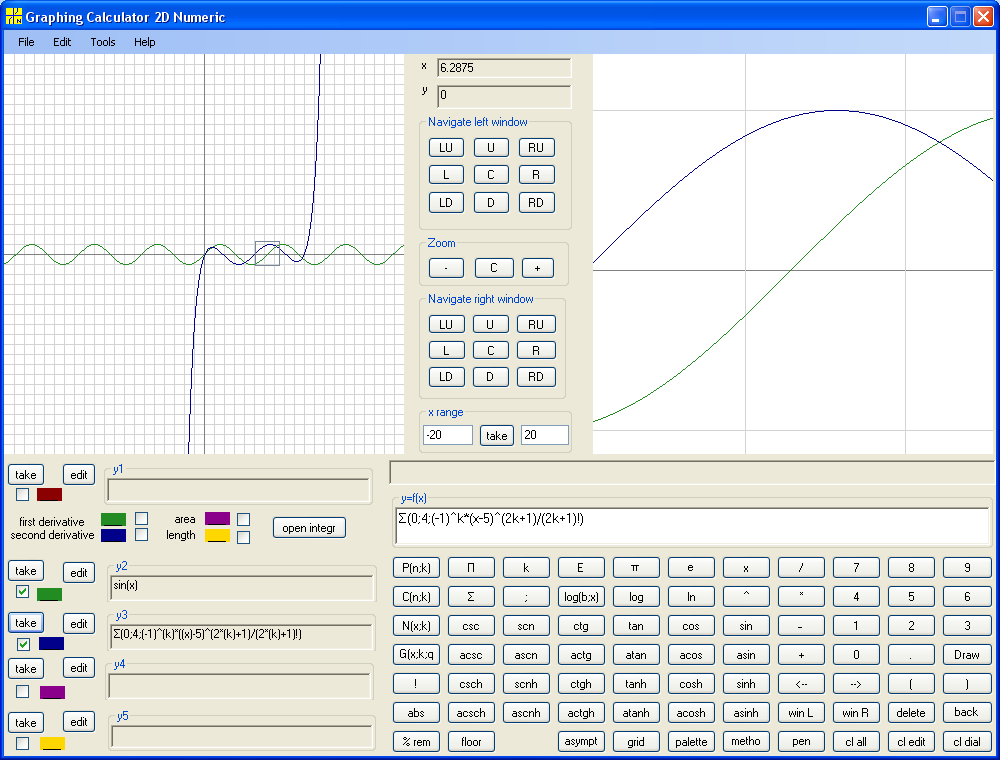
We see that the polynomial is not a good approximation of Sine anymore . What
is wrong? Replacing x by x-5 we make Maclaurin polynomial into Taylor
polynomial. But in Taylor polynomial for Sine at 5 the coefficient at member of
nth degree is not just (-1)^n, what is alternating Sine and Cosine at zero,
but alternating Sine and Cosine at 5. To remedy the situations let's shift by
multiple of 2π . Then the coefficients are again (-1)^n . Shift by 2π to
the left:
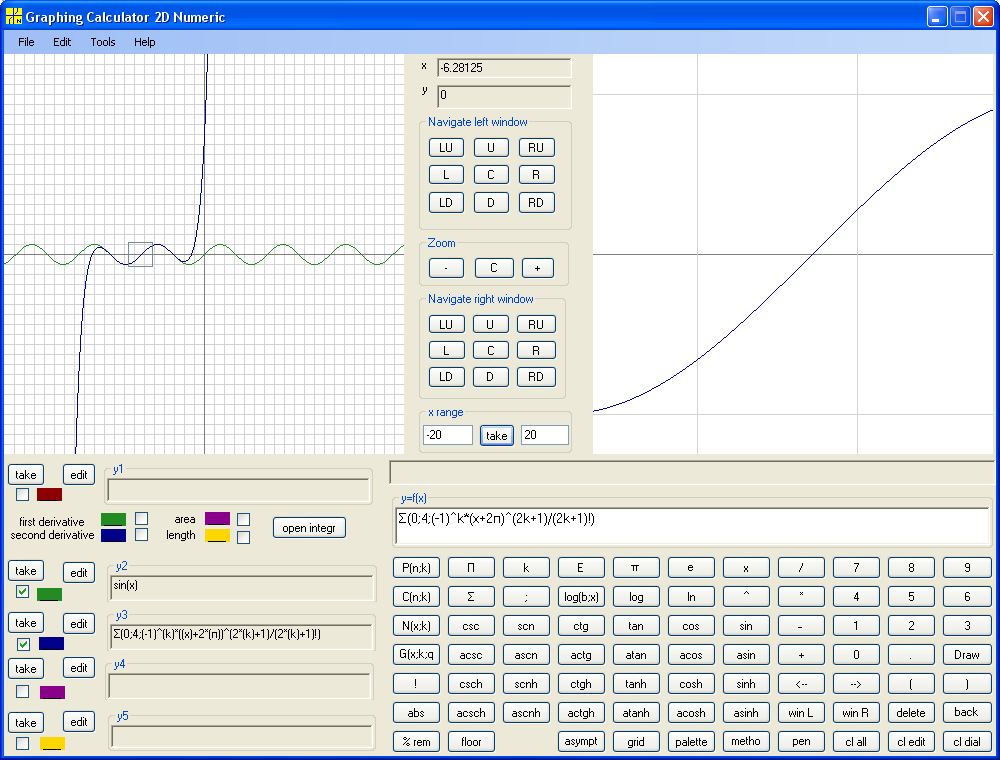
Shift by 2π to the right :
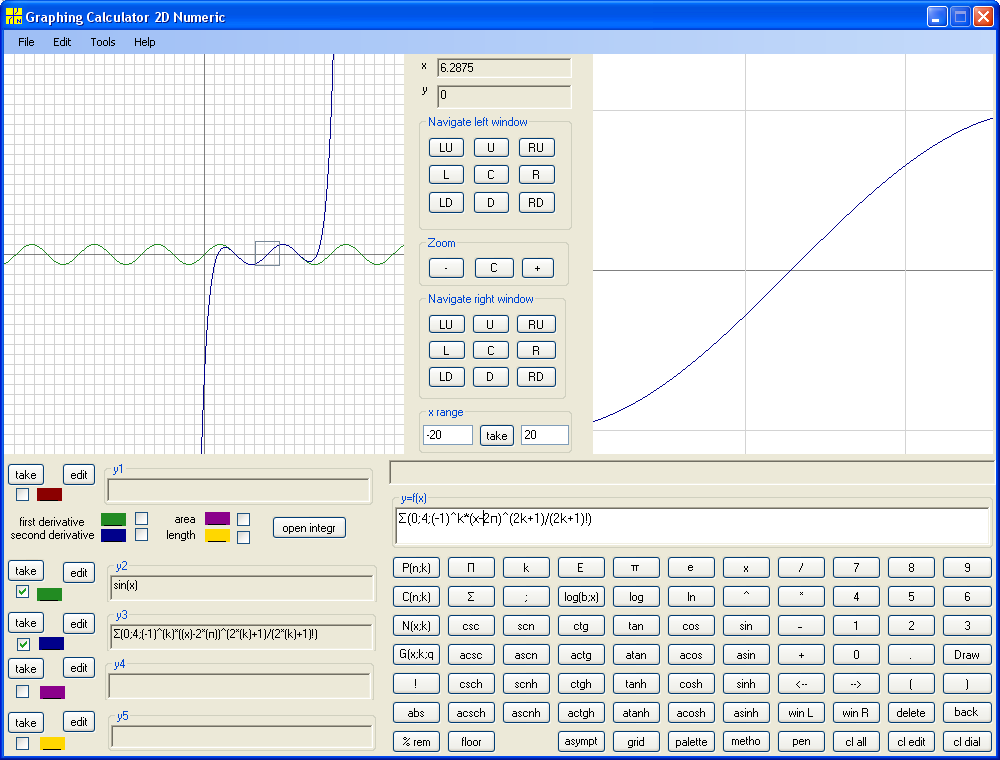
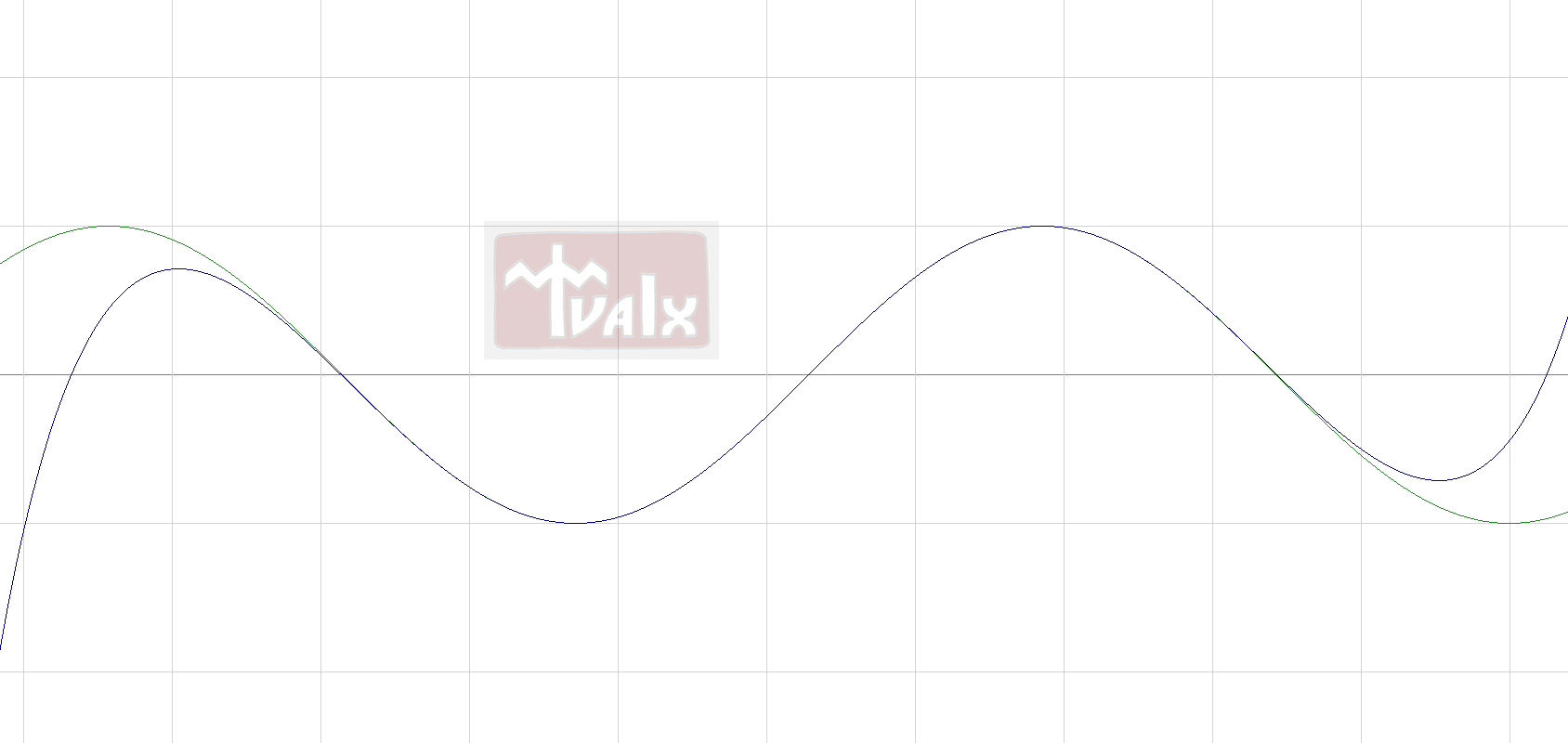
So for a good approximation we first find nearest to given x multiple of 2π .
Then calculate corresponding Taylor polynomial with some (not very high) degree. From
the picture below we can see that even forth degree gives not bad approximation:
© 2008 Tvalx

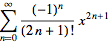 .
Let's compare graph of Sine with graphs of Maclaurin polynomials of different
degree for Sine. In terms of Graphing
Calculator 2D Numeric the Maclauren polynomial for Sine is Σ(0; degree;
(-1)^k*x^(2k+1)/(2k+1)!) . Even the polynomial of zero degree, that is y=x, is a
good approximation near the origin .
.
Let's compare graph of Sine with graphs of Maclaurin polynomials of different
degree for Sine. In terms of Graphing
Calculator 2D Numeric the Maclauren polynomial for Sine is Σ(0; degree;
(-1)^k*x^(2k+1)/(2k+1)!) . Even the polynomial of zero degree, that is y=x, is a
good approximation near the origin .










