Mathematical Software. Mathematical Research. Mathematical Education. Tvalx Products.
Let's explore Lower Incomplete Gamma function using Math Center Level2.
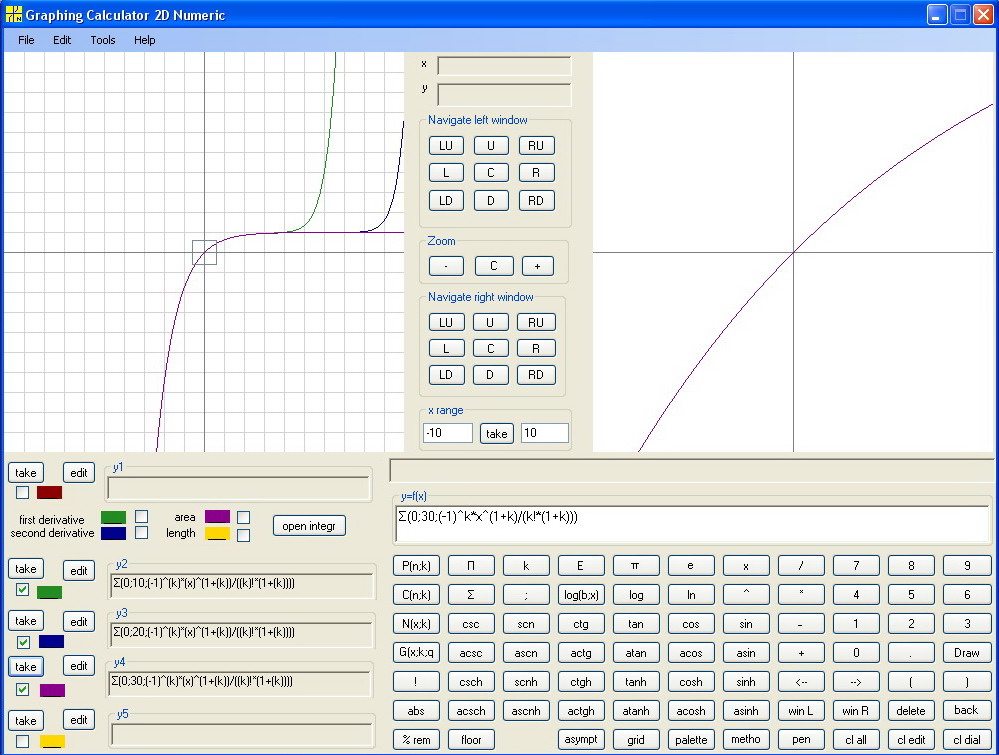
The Lower Incomplete Gamma function is defined by infinite series Σ(0; infinity; (-1)^k*x^(a+k) / (k!*(a+k)) ) . So, start with a=1 . Take upper limit of index 10, 20, 30 . Copy text below into Edit Window of Graphing Calculator Numeric of Math Center Level 2 :
Σ(0;10;(-1)^k*x^(1+k)/(k!*(1+k)))
Σ(0;20;(-1)^k*x^(1+k)/(k!*(1+k)))
Σ(0;30;(-1)^k*x^(1+k)/(k!*(1+k)))
After a couple of minutes we get the general picture from which we can conclude that the bigger upper limit we take the later on the right the graph goes up. So we can expect that with infinite upper limit the graph never goes up and stays at y=1 :

As we have seen the upper limit 30 or 40 gives enough precise picture in x range -10, 10 . Let's vary a. Take a = 1, 2, 3, 4 :
Σ(0;30;(-1)^k*x^(1+k)/(k!*(1+k)))
Σ(0;30;(-1)^k*x^(2+k)/(k!*(2+k)))
Σ(0;30;(-1)^k*x^(3+k)/(k!*(3+k)))
Σ(0;40;(-1)^k*x^(4+k)/(k!*(4+k)))
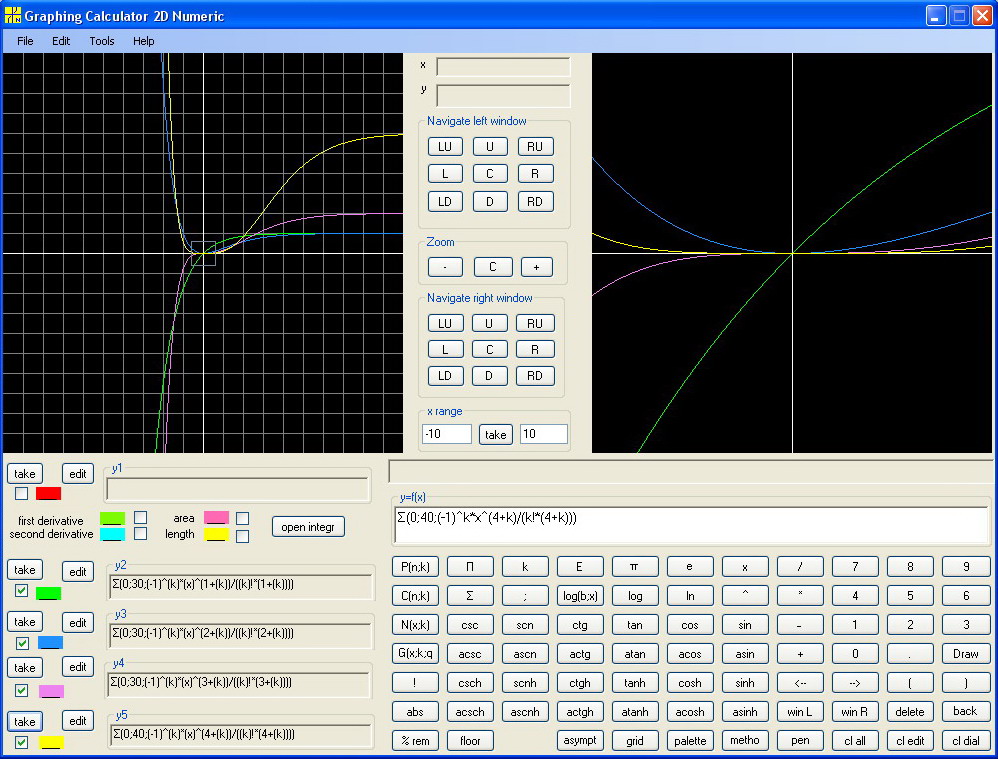
Zoom twice and open Left Window:
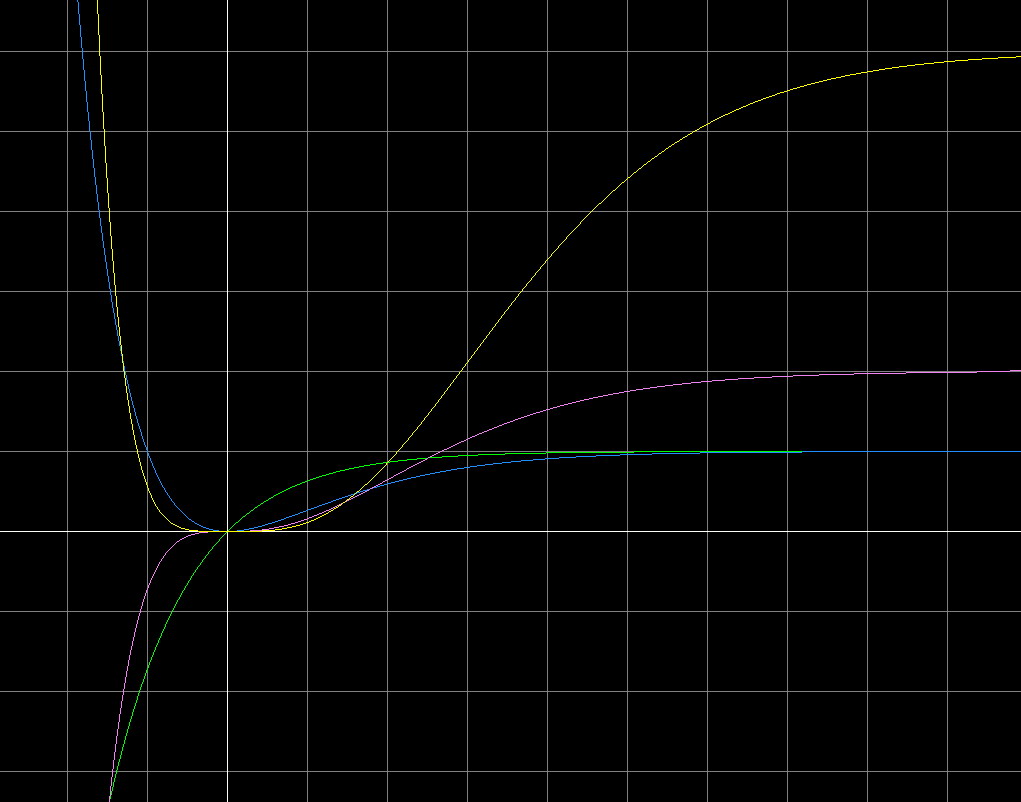
As we see, all graphs goes through the origin. They goes sharply up or down on the left, depending if the a is even or odd, and they are approaching horizontal line y=(a-1)! on the right.
Now take a = 0, -1, -2, -3 . We get an empty picture. Plug formula Σ(0;30;(-1)^k*x0^(a+k)/(k!*(a+k))) into Scientific Calculator Precision 72 and vary variable x0 and user constant a. We get Infinity. So the Lower Incomplete Gamma function has singularity at zero and negative values of parameter a. This is plausible since for k=-a we get a member of summation with zero denominator.
Take a = -1.5, -0.5, 0.5, 1.5 :
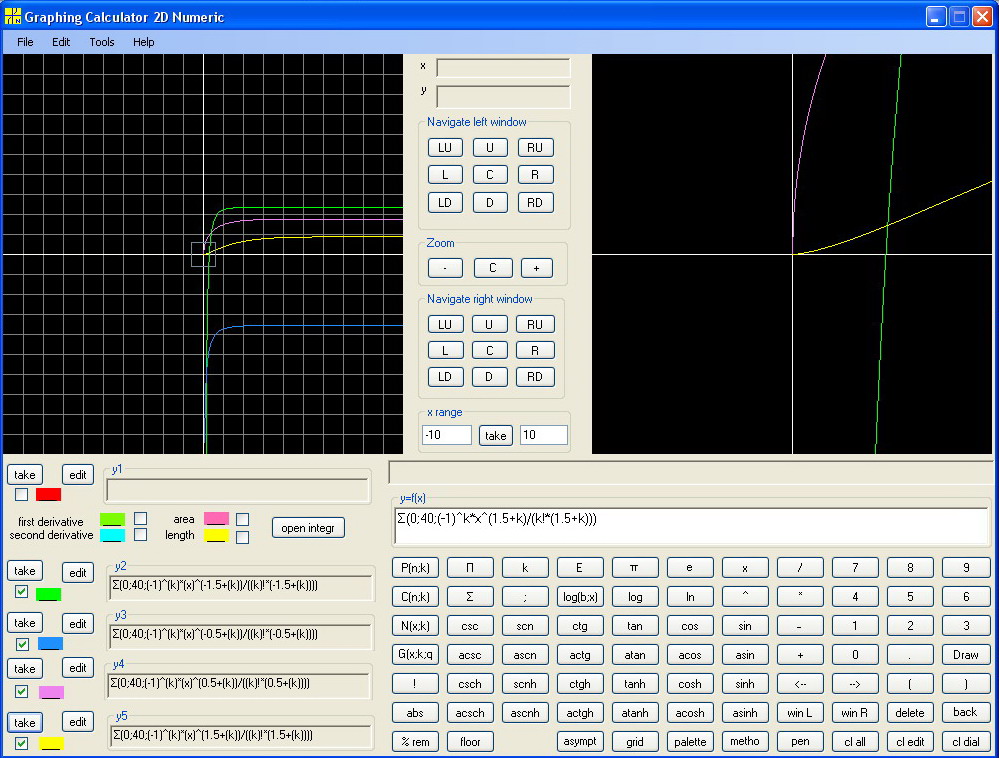
The picture is somewhat complicated. We might expect that since the function has singularities at non-positive integers. For full exploration we need a graphing calculator 6D ( a complex function with two variables).
Let's make x in LIGamma(a;x) a parameter and make the a a continuous variable. So x in Graphing Calculator 2D Numeric is now the a from LIGamma(a;x). Take x=0.5, 1, 5, 10 :
Σ(0;40;(-1)^k*0.5^(x+k)/(k!*(x+k)))
Σ(0;40;(-1)^k*1^(x+k)/(k!*(x+k)))
Σ(0;40;(-1)^k*5^(x+k)/(k!*(x+k)))
Σ(0;40;(-1)^k*10^(x+k)/(k!*(x+k)))
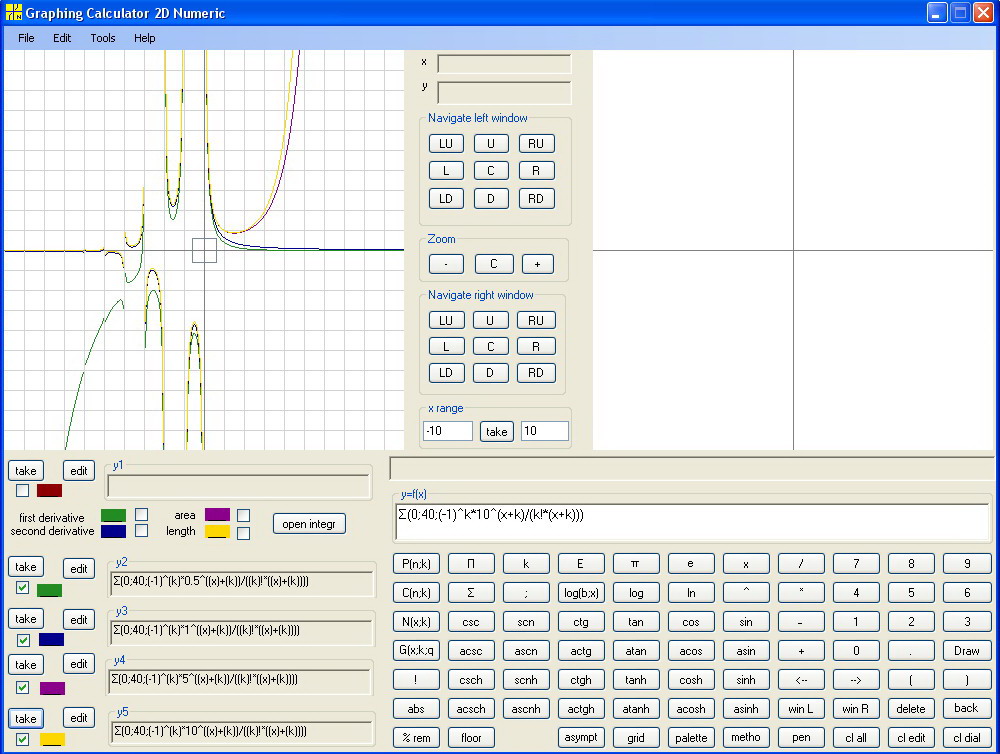
Mark in Tools menu options Anti Alias and High Quality, zoom twice, change palette, and open left window.
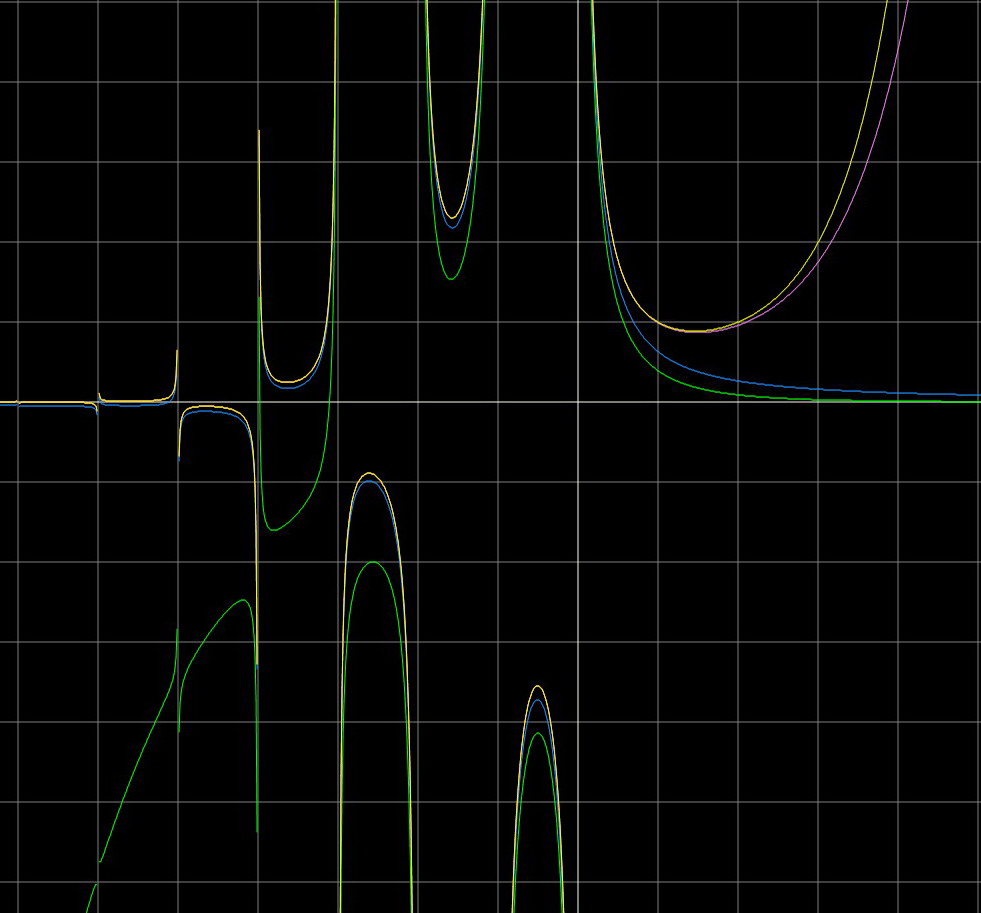
The picture approaches the graph of Gamma function when x goes to infinity.
© 2008 Tvalx
