Mathematical Software. Mathematical Research. Mathematical Education. Tvalx Products.
The tanh-sinh quadrature scheme was was developed by Takasi and Mori: Takahasi, Hidetosi; Mori, Masatake (1974), "Double exponential formulas for numerical integration", Publications of the Research Institute for Mathematical Sciences 9 (3): 721–741
The latest publication : David H. Bailey, Karthik Jeyabalan, and Xiaoye S. Li, "A comparison of three high-precision quadrature scheme". Experimental Mathematics, 14.3 (2005).
We have done our own research with help of Quadrature Calculator Precision 90.
The scheme worked very well for large variety of smooth functions. Even for functions with growing derivatives at end points.
The scheme failed to converge with Gamma function.
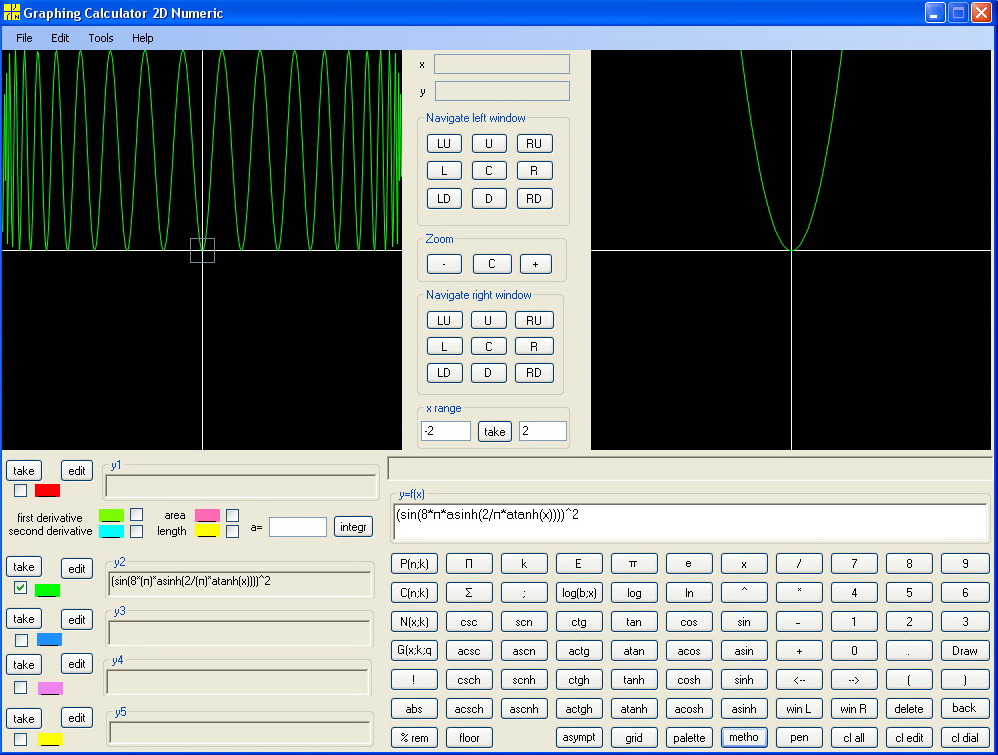
A special function was constructed to show that the scheme sometimes gives wrong answer. Namely f(x) = (sin(8*π*asinh(2/π*atanh(x))))^2 . The scheme gives result close to zero. It was predictable because the functions has zero value at points where the scheme calculates at level 1 and 2 . But the actual integral is not close to zero. See its graph:

In publication "Tanh-Sinhn High-Precision Quadrature" David H. Bailey1 19 Jan 2006, David Bailey gives error estimation h*(h/(2π))^2*Σ(-n;n;f''(k*h)). David Bailey considers it as "highly accurate" .In experiment we got by this formula 4.2E-5 for cos(x) on [-1, 1] at level 5 with actual accuracy 15 digits and corresponding uncertainty 5.0E-15 . At level 6 it would be 1E-5 and at level 7 (actual accuracy more than 90 digits) it would be 2.5E-6. Indeed, h*Σ(-n;n;f''(k*h))/(2π)^2 does not change significantly and h^2 is divided by 4 at each level. Such estimation is far from being "highly accurate".
Conclusion. The tanh-sinh quadrature scheme converges quickly and accurately for large variety of functions with few exceptions. There is no practical universal error estimation procedure. When the algorithm converges "normally", the difference between levels sums is a practical error estimation.
© 2008 Tvalx
