Mathematical Software. Mathematical Research. Mathematical Education. Tvalx Products.
Scientific Calculator Decimal for Windows 98, Windows ME, Windows 2000, Windows Server (2000, 2003, 2008, 2012), Windows XP and Vista
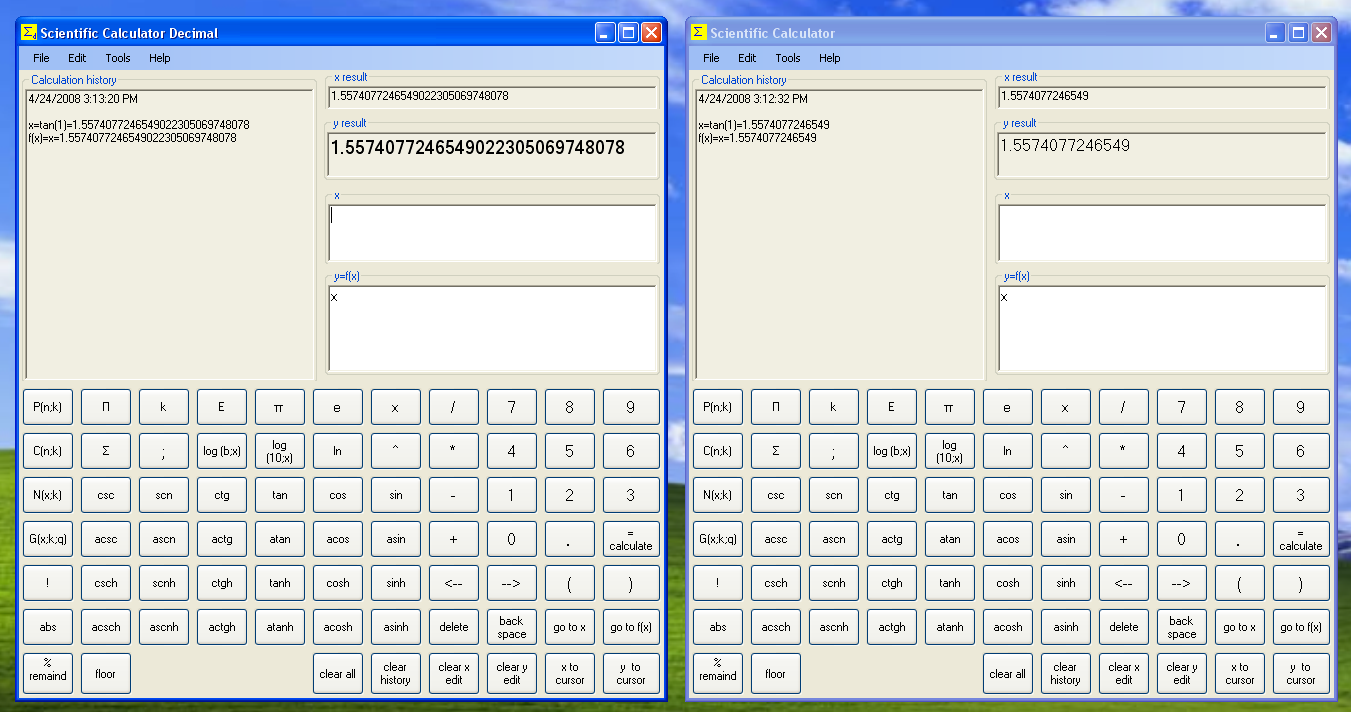
Scientific Calculator Decimal is programmed in C# and is similar to Scientific Calculator from Math Center Level 2 except that all calculations are done in decimal data type instead of double. Each calculator has its own advantages. Data type double can operate numbers with large exponent and decimal data type has twice longer mantissa. That is double has about 14-15 digits and decimal has 28-30 digits. Compare two calculators below:

Note that Editing Window, Result Window and History Window are just text-boxes. So you can apply standard operations of selecting, copying and pasting text. For this move mouse with left button pressed for selection, press Ctrl+C for copying, and Ctrl+V for pasting. Also you can save calculation history into a text-file, then later open that file in WordPad, select and copy long formula from the text and paste it into Editing Window.
There are four standard arithmetic operations buttons : + - * / . Clicking button "=" triggers calculation. If you are typing into the Edit Window from a keyboard, do not use Enter key for triggering calculation. It is not supported in Advanced Calculator.
There are two logarithms in Scientific Calculator Decimal. Enter ln(x) for natural logarithm of x, log(x) for decimal logarithm of x. For example, lg(10;100)=2 .
The Advanced Calculator supports all trigonometric functions: sin, cos, tan, ctg, arcsin, arccos, arctan, arctcg. In the Edit window arcsin, arccos, arctan, and arcctg are represented as asin, cos, atan, actg correspondently .
Button "%" represents remainder function. For example, if x = 2.4 then x % 1 = 0.4. If x = 5 then x % 2 = 1 . If x=7.8 then (x -x %1) = 7 .
Permutations are calculated according to formula P(n;k) = n! / (n - k)! . Note that despite this equality the calculation of P(n;k) is done much faster than calculation of n! / (n - k)! . This is because permutation has a known calculation algorithm, which is built into the program. Whereas the formula n! / (n - k)! calls the factorial procedure two times. Moreover n! grows fast with increase of n and can quickly cause overflow (overflow is a process of losing precision of calculations). Internal algorithm of P(n;k) does not create overflow. The same consideration applies to C(n;k), N(x;k), and G(x;k;q) .
Combinations are calculated according formula C(n;k) = n! / ( k! * (n -k)! ) . They are called also binomial coefficients, because they represents coefficients in polynomial (binomial).
The Newton polynomial is given by formula N(x;k) = x(x-1)(x-2)...(x-k+1)/k! . If x is given a real value, it becomes a generalized binomial coefficient. If x is a natural number n, it becomes C(n;k) .
G(x;k;q) are generalized Gaussian binomials called also Gaussian coefficients and q-binomial coefficients . The calculation formula is G(x;k;q) = (1-q^x)(1-q^(x-1))...(1-q^(x-k+1))/(1-q)(1-q^2)...(1-q^k) .
All calculations are done in C# decimal format. So the range of calculations is from ±1.0 × 10−28 to ±7.9 × 1028 and precision is 28-29 digits.
© 2008 Tvalx
